Die Trenneigenschaften des Empfangsgleichrichters

Als Mitte der '30er Jahre die AM Senderdichte immer dichter wurde und speziell in Europa (Region 1) die Sender immer größere Leistungen hatten, ergab sich die Forderung nach immer höherer Trennschärfe der Empfänger.
Die Probleme waren sowohl das Interferenz-Pfeifen (9kHz Ton) durch die Trägerschwingungen der Sender in den beiden benachbarten Kanälen als auch das „Durchschlagen“ der Modulationsinhalte von (frequenzmäßig) benachbarten Sendern.

Es mußte eine kostenmäßig optimale Lösung für diese Schwierigkeiten gefunden werden. Eine Vergrößerung der Anzahl der Schwingkreise bzw. der Bandfilter in den Zwischenfrequenzstufen u.a mit regelbarer Bandbreite kam nur für „Luxus-Geräte“ in Betracht. Für einfachere Geräte waren kostenmäßig billigere Lösungen erforderlich.

Das führte zu einer Analyse der Funktionsweise der einzelnen Stufen eines Empfängers mit dem Ziel, eine Problemlösung zu finden. Gemäß „Pitsch, H.: Lehrbuch der Funkempfangstechnik, VAG“ hat hierbei insbesondere O. Tüxen 1941 den „Einfluß des Gleichrichters auf die Trennschärfe des Empfängers“ untersucht, sowie H. Roder 1938 die „Modulation Suppression of a weak Signal by a stronger one“. Auch H. Buchmann hat 1941 einen Aufsatz über „Die neuere Entwicklung bei der Gleichrichtung amplitudenmodulierter Träger“ verfaßt.

Das ist zunächst einmal verblüffend, weil ein Gleichrichter ja eigentlich keine Filterwirkung hat.

Eine AM Demodulatorschaltung mit einem Gleichrichter (Diode, Detektor), ein so genannter Hüllkurven-Demodulator, findet sich Ende der '30er Jahre in (fast) jedem Radio. Bei Supern ist es die letzte Stufe im Zwischenfrequenzteil, die von ihrer Schaltung große Ähnlichkeit mit dem Detektor aus der Anfangszeit des Radios hat.

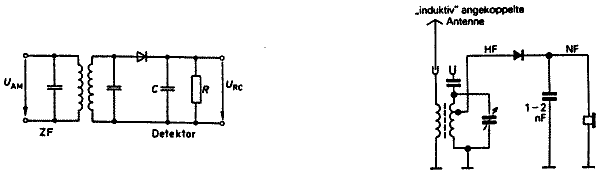
Die Gleichrichter-Diode trennt den HF-Teil (links) vom NF-Teil (rechts).
Der HF-Teil muß dabei so ausgeführt sein, daß an ihm keine NF-Spannung und keine Gleichspannung abfällt. Dies erreicht man durch die Spule des Schwingkreises, die Gleichstrom- und NF-mäßig kurzschließt. 
Andererseits muß der NF-Teil so ausgelegt sein, daß an ihm keine HF-Spannung abfällt. Dies erreicht man durch den Kondensator C. Die NF muß andererseits an diesem C abzugreifen sein. Daher benötigt man einen Entlade-Widerstand R parallel zu C. Die Zeitkonstante T=RC muß so gewählt sein, daß die Entladung der NF folgen kann.

Die Demodulation, d.h. die „Abtastung“ der Hüllkurve der AM-Schwingung zeigt das nächste Bild.

Wie zu erkennen ist, muß die Zeitkonstante des RC-Tiefpasses des „Detektors“ geeignet gewählt werden. Ist diese zu klein, hat das demodulierte Signal eine zu große HF Restwelligkeit. Ist diese aber zu groß, folgt die Ausgangsspannung nicht mehr der Hüllkurve der AM, sondern „hebt ab“, wodurch sich (nichtlineare) Verzerrungen des demodulierten Signals ergeben.
Der RC-Tiefpaß ist zwar eine lineare Schaltung. Aber im Zusammenspiel mit der Diode ergibt sich ein nichtlineares Verhalten, wenn die Zeitkonstante zu groß gewählt ist.

Es soll jetzt der Fall betrachtet werden, daß ausschließlich die Trägerschwingungen des gewünschten Senders (mit größerer Amplitude A) und die eines nicht gewünschten Senders (mit kleinerer Amplitude a) des Nachbarkanals an der Diode anliegen. Diese beiden Trägerschwingungen ergeben dann eine „Schwebung“.

Die sich ergebende Zeitfunktion der Schwebung hat gewisse Ähnlichkeit mit einer amplitudenmodulierten Schwingung (AM). Der Hüllkurven-Demodulator tastet diese Hüllkurve ab, wodurch sich eine „demodulierte“ Spannung mit der Frequenz 9kHz ergibt, nämlich dem Frequenzunterschied der beiden Trägerschwingungen. Das ist ein Pfeifton, der als Träger-Interferenz bezeichnet wird. Seine Lautstärke hängt davon ab, wie groß die Amplitude des Trägers aus dem Nachbarkanal am Detektor ankommt.

Aber der Interferenzton ist kein reiner Sinuston. Seine Form weicht um so mehr vom Sinus ab, je mehr sich die Amplituden der beiden Träger gleichen. Das ist deutlich zu sehen, wenn beide Amplituden gleich sind (m_E=1).

[Bei der Demodulation von Einseitenband Signalen (auf Kurzwelle) bestehen ähnliche Verhältnisse. Dem SSB-Signal wird (lokal) ein Träger großer Amplitude hinzugefügt, so daß der resultierende Modulationsgrad z.B. m_E=0,2 wird. Damit erhält man eine fast verzerrungsfreie Demodulation.]

Die Abweichung vom Sinus-Verlauf bei der „Demodulation“ einer Schwebung ist der Schlüssel zum Verständnis der Trenneigenschaft eines Detektors bzw. Gleichrichters.

Hierzu werden die Zeitverläufe der Spannungen am Sekundärkreis des ZF-Bandfilters, also vor der Detektordiode betrachtet. Der Träger des Nutz-Senders habe die Amplitude A, während der Stör-Sender (des Nachbarkanals) noch mit der Amplitude a ankommt. Ferner sei angenommen, daß der Nutz-Sender unmoduliert sei und der Störsender im rechten Teil des nächsten Bildes moduliert sei.

Im linken Teil des Bildes entsteht eine Schwebung aus dem Träger des Nutz-Senders und dem des Stör-Senders. Wäre der Verlauf der Hüllkurve der Schwebung genau sinus-förmig, fiele der Mittelwert M der Schwebung mit der Amplitude A des Nutz-Trägers zusammen. Weil die Einhüllende der Schwebung jedoch für kleine Werte spitziger zuläuft, wird M größer als A (Maßstab in der Skizze übertrieben).
Ist nun im rechten Teil des Bildes der Stör-Sender moduliert, so überträgt sich diese Modulation auch auf den Mittelwert M, hier als M_N bezeichnet, während bei exakt sinusförmigem Verlauf der Schwebung die Modulation des Stör-Senders unterdrückt wäre.

In der Abb. 404 ist nun unterstellt, daß die RC-Zeitkonstante des Demodulators so klein gewählt ist, daß der 9kHz Interferenzton voll durchkommt.
Alternativ könnte man sich überlegen, die RC-Zeitkonstante so groß zu wählen, daß die demodulierte Spannung hierfür „abhebt“ und somit die 9kHz Schwingung (mehr oder weniger) ausgeglättet wird, entsprechend zu der Hüllkurve U in der Abb. Nur dann zeigt sich der kuriose Fall, daß die Modulation U_N des Störsenders (im rechten Teil der Abb.) nunmehr voll durchkommt.
Man hat also die Wahl zwischen zwei Übeln: Entweder der 9kHz Interferenzton kommt voll durch oder die Modulation der Sender in den unmittelbaren Nachbarkanälen.
[Die Sender in den weiter abliegenden Kanälen werden im ZF Filter ausreichend geschwächt.]

Man hat sich dafür entschieden, die Modulation der Nachbarkanäle im Demodulator zu unterdrücken. Die Unterdrückung des 9kHz Interferenztones geschieht mit Hilfe eines Sperrkreises bzw. eines Kurzschlußkreises, der i.a. an der Anode der Endröhre angeschlossen ist.

Ist der Stör-Sender am Demodulator stärker als der Nutz-Sender, erfolgt praktisch keinerlei Unterdrückung der Stör-Modulation, wie das nächste Bild zeigt.

Die Schlußfolgerung daraus ist, daß das Signal des Nutz-Senders am Demodulator größer sein muß als das Signal des Nachbarkanal-Senders, damit die „Trenneigenschaften“ des Demodulators zur Wirkung kommen. Das heißt, daß die Selektion des HF- und ZF-Teils eines Empfängers so gut sein muß, daß die Sender der (unmittelbaren) Nachbarkanäle schwächer ankommen als der Nutz-Sender.

Für diesen Fall kann man die Abbildungen 406 und 404 auch anders herum interpretieren, nämlich, daß der Nutz-Sender die Amplitude a hat und der Stör-Sender die Amplitude A. Man sieht dann, daß in Abb. 406 die gewünschte Modulation M_N praktisch ungeschwächt bleibt, während sie in Abb. 404 durch den Störer geschwächt wird.

Tatsächlich bedeutet dies, daß es auch bei AM (infolge der Gleichrichtung) eine gegenseitige Unterdrückung der Nachbarkanäle gibt, wobei das stärkere Signal „siegt“.

Wenn der gewünschte Sender A stärker ist als der Störsender a (A/a > 1) , wird die Modulation des störenden Senders geschwächt.

[Bei Frequenzmodulation (FM) gibt es einen ähnlichen Effekt, der hier als „Capture-Ratio“ bezeichnet wird. Bei FM ist der Modulationsprozeß selbst nichtlinear, weshalb sie auch als „exponentielle Modulation“ bezeichnet wird. Eine gegenseitige Unterdrückung der Modulation gibt es immer dann, wenn Nichtlinearitäten beteiligt sind.]

Aufgrund der Nichtlinearität des Spitzengleichrichters als AM-Demodulator ergibt sich die (wenig bekannte) Eigenschaft, daß bei geeigneter Dimensionierung des Empfängers, die Filterwirkung bezüglich Nachbarkanalstörungen verbessert wird. De facto wirkt es sich aus, als ob die Bandfilter des Empfängers eine größere Flankensteilheit hätten.
Das gilt aber nur für die unmittelbaren Nachbarkanäle. Die weiter entfernten Kanäle ergeben so hohe Interferenztöne, daß hierfür die RC Zeitkonstante des Demodulators zu groß ist. Das ist jedoch kein gravierender Nachteil, weil die weiter ab liegenden Kanäle durch die HF- und ZF-Filter des Empfängers ausreichend gedämpft werden können.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Während der "normale" AM-Demodulator die Glättung der HF "nur" mit Hilfe eines Tiefpasses erreicht, ist beim Grundig 5040W das Lade-C durch eine Reaktanz-Schaltung ersetzt, bestehend aus der Serienschaltung von C und Parallelschwingkreis.

Die "normale" HF-Glättung mit RC-Glied:

Schaltungsauszug Grundig 5040W:

Rot eingerahmt oben ist diese Reaktanz-Schaltung.

Angaben zum Frequenz-Verlauf des Widerstandes dieser Reaktanzschaltung findet man in "Henney, K.: "Radio Engineering Handbook, 5^th ed., McGraw-Hill, 1959"

Hier ist also zu erkennen, daß der Impedanzverlauf dieser Schaltung bei einer tieferen Frequenz f₁ einen Kurzschluß darstellt (Serien-Resonanz), während bei einer höheren Frequenz f₂ Leerlauf besteht (Parallel-Resonanz).

Um zu erkennen, wie sich dieser Reaktanzzweipol auswirkt, wurde die Schaltung mit LTspice© simuliert. Es wurden nur die im Schaltbild rot eingerahmten Teile berücksichtigt. Für den AM-Demodulator (Diode) wurde ersatzweise nur ein Innenwiderstand von 100kΩ angesetzt.

Die Werte für die Spule L=0,62Hy, R=730Ω hat Hans Knoll ermittelt. Vielen Dank!

 

In dem Sweep sind die Spannung am Schwingkreis V(n001) und die Spannung an R3 V(n004) dargestellt.

Wie zu sehen ist, wurde die Serienresonanz (Nullstelle) auf 9kHz festgelegt und ist damit tiefer als die Parallelresonanz (Polstelle) - in Übereinstimmung mit dem theoretischen Verlauf der Reaktanz.

Hans Knoll hat berichtet, daß die Schaltung des 5040W von einem hervorragenden Entwicklungs-Ingenieur stammt, der theoretisch gut beschlagen war - und das auch praktisch umsetzen konnte.

Der Vorteil der Schaltungsanordnung besteht u.a. auch darin, daß die 9kHz Sperre tatsächlich nur im AM-Zweig wirkt und deshalb bei UKW nicht abgeschaltet werden muß.

Beim 5040W ist die Induktivität der 9kHz Sperre unter dem Chassis zu finden.

Es ist die etwas "schief" in der Gegend liegende Zylinderspule rechts unten in diesem Bild. Die beiden 250pF Kondensatoren sind ebenfalls oberhalb der Spule zu sehen. Der Platz und die Lage der Spule sind mit Bedacht gewählt: schließlich darf sie kein Brummen "einsammeln".

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Beim Grundig_5040W_3D wurde die Reaktanzschaltung gegenüber dem 5040W verändert.

Hier ein Ausschnitt des Schaltbildes, der die Beschaltung des Reaktanznetzwerks im roten Rechteck oben zeigt. Abgesehen davon, daß die Werte von C92 und C102 gegenüber dem 5040W geändert sind, gibt es hier zusätzlich den Kondensator C103, der auf den Summenpunkt geführt ist, von welchem das NF-Signal abgenommen wird.

In der LTspice Schaltung, die die wesentlichen Schaltelemente in den beiden roten Rechtecken enthält, ist der Signalweg über C103 (C4 = 75pF) deutlicher zu sehen.

Der mit LTspice berechnete Frequenzgang der Schaltung läßt erkennen, daß durch den zusätzlichen Signalweg über die 75pF eine deutliche Versteilerung des Notch-Filters gegnüber dem 5040W erreicht wird.

Die Analysen lassen erkennen, daß diese Empfänger nicht nur im UKW-Teil, sondern auch im AM-Teil einige Besonderheiten aufweisen.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Nach der hervorragenden Einführung in die Thematik durch Herrn Prof. Rudolph möchte ich an dieser Stelle noch eine Ergänzungen bringen. Es geht dabei um die quantitative Berechnung der Unter-drückung der Modulation eines Störsenders, sowie um die Trenneigenschaften von nichtlinearen Hüllkurvendetektoren, die im ersten Beitrag noch nicht angesprochen wurden.

Zunächst kurz zur Terminologie: Im Folgenden wird der gewünschte Sender, auf den der Empfänger eingestellt wurde, als Nutzsender "a" bezeichnet, ein frequenzmäßig benachbarte Sender (Abstand 9kHz für LW und MW in Europa) wird als Störsender "b" bezeichnet.

Zur quantitativen Berechnung des Durchschlagens der Modulation eines Störsenders ist zunächst ein
formelmäßiger Ausdruck für die Hüllkurve der Schwebung (siehe Abb. 41 im ersten Beitrag), die sich aus Nutzsignal a und Störsignal b ergibt, notwendig. Dieser ist leicht herzuleiten: (Der mathematisch weniger interessierte Leser kann sich auf die Darlegung des Problems in Gleichung (1) und das Ergebnis in Gleichung (2) beschränken)

Maximum und Minimum der Hüllkurve ergeben sich aus Gleichung (2) erwartungsgemäß zu a+b bzw. a-b. Ist die Zeitkonstante des Hüllkurvendetektors so groß, dass eine Spitzenwertdetektion der Hüll- kurve erfolgt, so liefert der Hüllkurvendetektor den Wert a+b. Nutzsignal und Störsignal sind damit quantitativ gleichberechtigt und es findet keine Unterdrückung der Modulation des Störsenders statt. Dies wurde im vorherigen Beitrag auch ausführlich erläutert.

Um eine Unterdrückung der Modulation des Störsenders zu erreichen, muss die Zeitkonstante des
Hüllkurvendetektors klein genug sein, um die Schwebung der Frequenz 9kHz (Frequenzabstand Nutz- sender zu Störsender) in der Hüllkurve auszumitteln. Siehe dazu auch Abb. 404 im ersten Beitrag. Diese Ausmittelung ist grafisch so zu verstehen, dass für die Fläche zwischen Hüllkurve und Zeit- achse über eine Periodendauer T der Schwebung eine Quadratur durchgeführt wird. D.h. es wird der (konstante) Mittelwert gesucht, mit dem das Rechteck zwischen Mittelwert und Zeitachse über eine Periodendauer T der Schwebung die selbe Fläche hat wie die Fläche zwischen Hüllkurve und Zeit- achse. Dies ist in der folgenden Abbildung nochmals verdeutlicht.

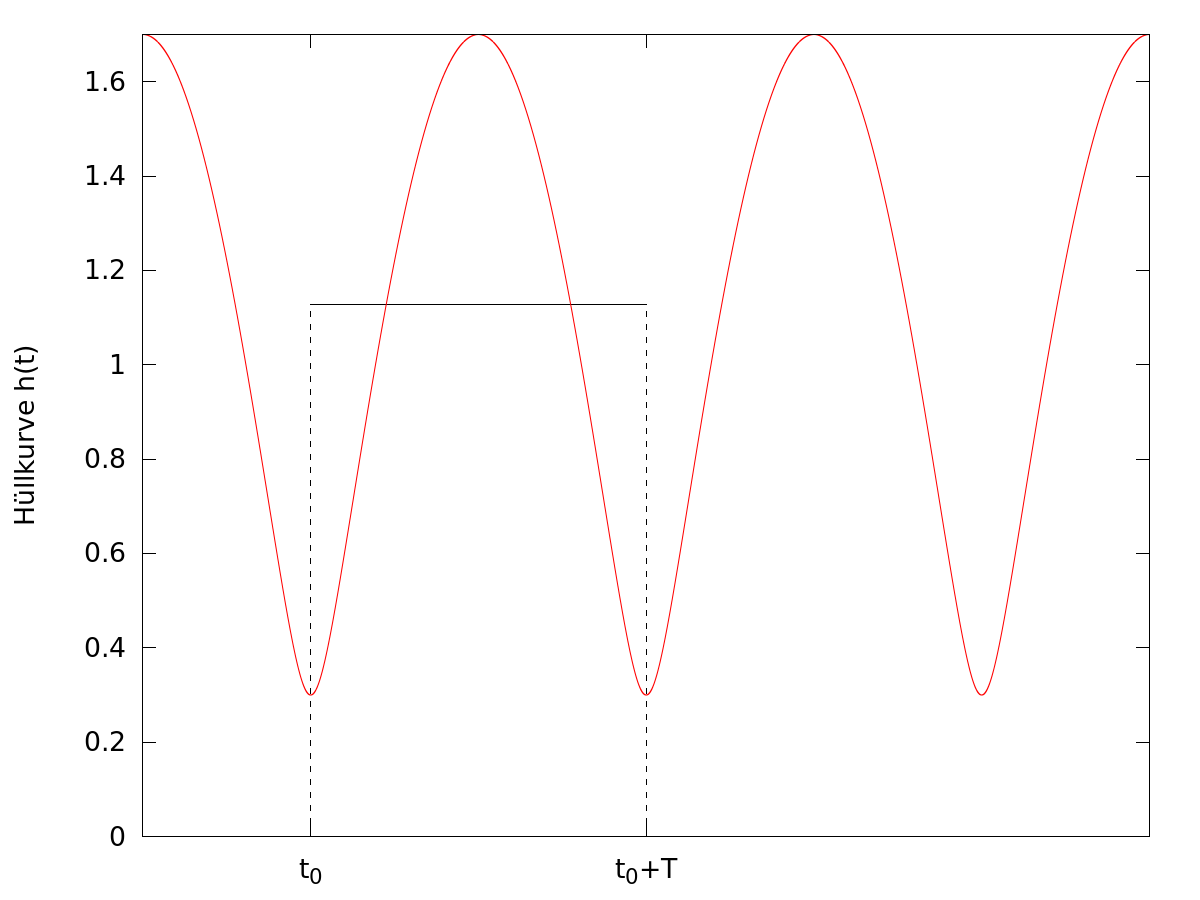
Da die Amplituden a und b des Nutz- bzw. Störsenders aber nicht konstant, sondern mit einer Ton- frequenz amplitudenmoduliert sind, muss noch zu folgender Näherung gegriffen werden: Die Frequenz der Schwebung ist wie bereits erwähnt 9kHz, die meisten vorkommenden Tonfrequenzen haben allerdings eine deutlich niedrigere Frequenz (z.B. 200Hz-2kHz). Die Amplituden a und b können daher über eine Periode T der Schwebung als näherungsweise konstant angesehen werden, was die Berechnung des Mittelwerts signifikant vereinfacht. Analytisch wird die Mittelwertbildung durch Integration der Hüllkurvenfunktion h(t) über eine Periode der Schwebung und Division durch die Periodendauer T vorgenommen:

Das resultierende Integral ist allerdings alles andere als trivial. Durch eine Substitution v(x)=sin(x)
kann das Problem zwar rein formal gelöst und mit Hilfe der elliptischen Integralfunktionen eine relativ
komplizierte Stammfunktion angegeben werden, in der Praxis ist die numerische Integration für konkrete Werte von a und b aber die bessere Alternative.

Um nun die Unterdrückung des Störsenders quantifizieren zu können, benötigt man erst mal ein Maß für die Stärke, mit der sich die Modulation Störsenders bei Empfang des Nutzsenders bemerkbar macht. Ein einfaches und sinnvolles Maß hierfür ist die absolute NF (Tonsignal) Ausgangsspannung U_NF des Störsenders am Hüllkurvendetektor bei Amplitudenmodulation des Störsenders mit einem sinusförmigen Tonsignal und unmoduliertem Nutzsender. Diese absolute NF Ausgangsspannung bestimmt letztendlich, wie laut der Störsender in den Sprech- bzw. Musikpausen des Nutzsenders zu hören ist. Die vom Störsender gelieferte NF Ausgangsspannung ist unter der weiter oben eingeführten Näherung für Tonfrequenzen deutlich unter 9kHz leicht zu berechnen:

Damit lässt sich unter Zuhilfenahme numerischer Verfahren zur Berechnung der auftretenden Integrale
die Unterdrückung der Modulation des Störsenders nun quantitativ untersuchen. Wir legen dazu die
Amplitude b₀ des Störsenders auf 1Vp fest. Die Amplitude a=a₀ des Nutzsenders (unmoduliert, da
Sprech- oder Musikpause angenommen wird) soll in einem Bereich von 0-3V_p variiert werden. Wir sind
nun in der Lage, die absolute NF (Tonsignal) Ausgangsspannung U_NF des Störsenders am Hüllkurven-detektor in Abhängigkeit vom Amplitudenverhältnis von Nutzsender zu Störsender für verschiedene Modulationsgrade des Störsenders zu berechnen und zu plotten.

Es ist deutlich zu erkennen, wie die Erhöhung der Amplitude des Nutzsenders tatsächlich eine
merkliche Unterdrückung der NF Ausgangsspannung des Störsenders zur Folge hat. Dies ist, wie bereits im vorherigen Beitrag sehr anschaulich erläutert, eine direkte Folge der Ausmittelung der
entstehenden 9kHz Schwebung zwischen den Signalen durch ein RC Glied mit geeigneter Zeit- konstante.

Wir wollen uns nun zum Abschluss noch dem Fall eines nichtlinearen Hüllkurvendetektors zuwenden, der auch im vorherigen Beitrag noch nicht besprochen wurde. Streng genommen ist natürlich jeder
Hüllkurvendetektor "nichtlinear", da dieser eine Gleichrichterfunktion haben muss um überhaupt als
Hüllkurvendetektor zu funktionieren. Die Eigenschaft nichtlinear bezieht sich in diesem Fall natürlich auf den Durchlassbereich der Gleichrichterfunktion und führt zu einer Verzerrung der resultierenden Hüllkurve. Die folgende Ausmittelung der Hüllkurve durch ein RC Glied mit geeigneter Zeitkonstante ist dagegen wieder linear.

Wir können für den nichtlinearen Hüllkurvendetektor im einfachsten Fall eine Kennlinie der Form
y=x^p für den Durchlassbereich x>0 ansetzen wie in der folgenden Abbildung gezeigt:

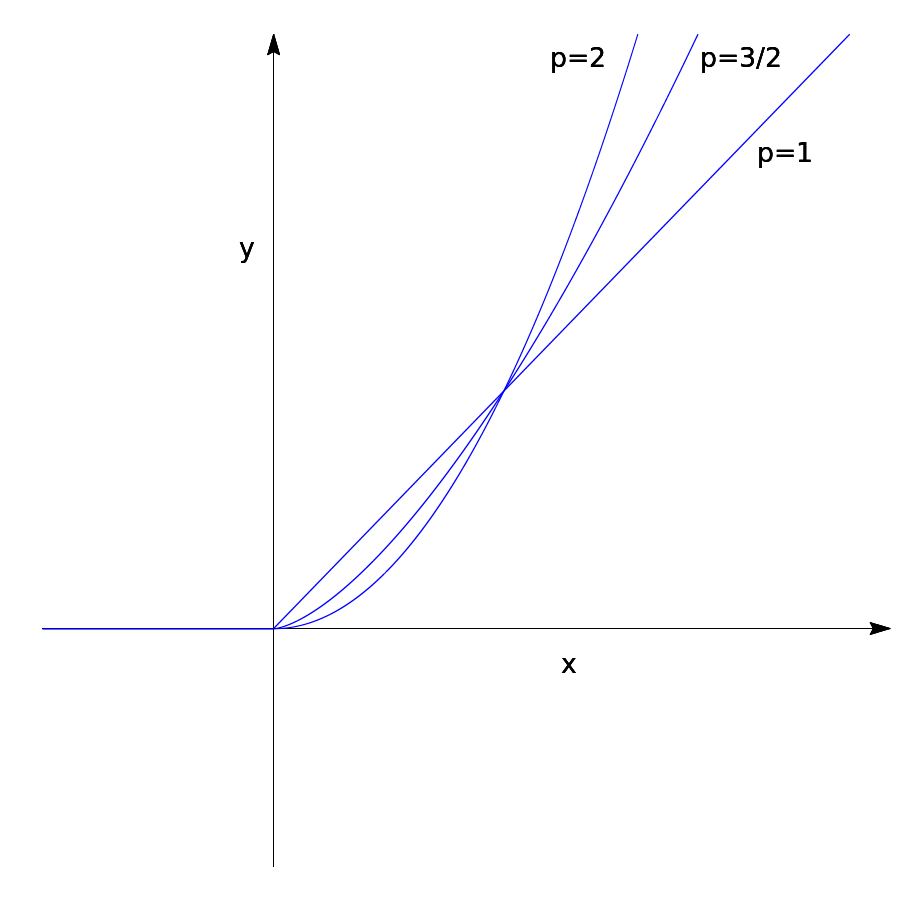
Die Erweiterung der oben dargelegten Rechnungen auf den nichtlinearen Fall ist sehr einfach durch
Anpassung der Hüllkurvenfunktion h(t) (vor der Glättung) zu bewerkstelligen:

Sehen wir und zunächst den Spezialfall p=2 an. In diesem Fall ist die Integration, welche die Aus- mittelung der Hüllkurve beschreibt trivial durchführbar, da dass Integral über die Cosinusfunktion
verschwindet und der Mittelwert der Hüllkurve über eine Periode der 9kHz Schwebung einfach a²+b²
ist. Genau wie im Falle der Spitzenwertdetektion der Hüllkurve durch ein RC Glied mit zu großer
Zeitkonstante sind Nutzsignal und Störsignal damit quantitativ gleichberechtigt und es findet keine
Unterdrückung der Modulation des Störsenders statt.

Der Fall p=3/2 ist ebenfalls von Interesse, da er grob die Verhältnisse bei Verwendung eines Anoden-gleichrichters (im Gegensatz zum üblicheren Gitter- oder Diodengleichrichter) beschreibt. Wir wollen daher die Unterdrückung der Modulation des Störsenders für diese Fälle mit der Unterdrückung der Modulation des Störsenders für den linearen Fall (p=1) vergleichen, in dem wir wiederum die absolute NF (Tonsignal) Ausgangsspannung U_NF des Störsenders am Hüllkurvendetektor in Abhängigkeit vom Amplitudenverhältnis von Nutzsender zu Störsender berechnen. Das Ergebnis ist für einen Modula-tionsgrad des Störsenders von 40% in der folgenden Abbildung dargestellt.

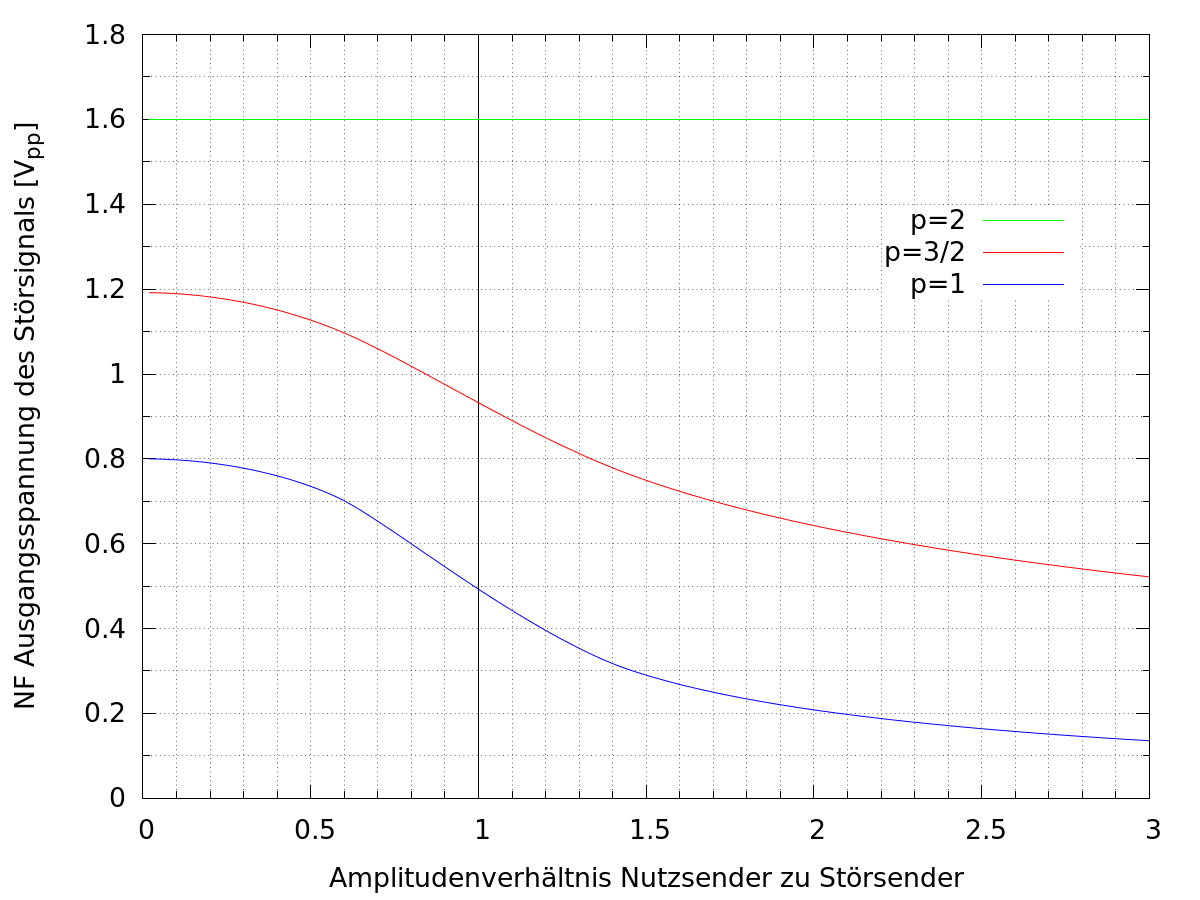
Durch das "Auseinanderziehen" der Hüllkurve auf der Spannungsachse durch den nichtlinearen
Hüllkurvendetektor ergibt sich zunächst eine Erhöhung der absoluten NF Ausgangsspannung des
Störsenders. Da dies aber auch für die absolute NF Ausgangsspannung des Nutzsignals geschieht, ist dies was die Trenneigenschaften angeht noch keine Nachteil. Allerdings ist aus dem Diagramm sehr schnell zu erkennen, dass das Absinken der absoluten NF Ausgangsspannung des Störsenders bei steigender Amplitude des Nutzsenders für den Fall p=3/2 deutlich langsamer als im linearen Fall (p=1) erfolgt. Z.B. ist bei einem Amplitudenverhältnis von Nutzsender zu Störsender von 2:1 die absolute NF Ausgangsspannung des Störsenders im linearen Fall auf fast 1/4 des ursprünglichen Wertes abgesunken, während sie sich im Falle p=3/2 nur ungefähr halbiert hat.

Für die Praxis lässt sich damit der Interessante Schluss ziehen, dass die Anodengleichrichtung
gegenüber der Gitter- bzw. Diodengleichrichtung neben den bekannten Nachteilen (Verzerrungen des
Tonsignals, keine negative Regelspannung für AVR) auch schlechtere Trenneigenschaften besitzt,
was sich natürlich insbesondere beim Einkreis-Geradeausempfänger bemerkbar macht.

 

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.