Grid-Dip-Meter, Falschanzeige?
? Grid-Dip-Meter, Falschanzeige?

Hallo allerseits,
im Zusammenhang mit einer unplausiblen Anzeige der Resonanzfrequenz eines Schwingkreises moechte ich hier fragen, ob es jemand schon erlebt hat, dass ein Dipper in der Praxis auch bei einer Oberwelle der Dipperfrequenz Resonanz anzeigt? Ich kann in meinem Falle leider weder Angaben ueber die Amplituden der (sicher existierenden) Oberwellen des Geraetes machen, noch ueber die Guete des zu messenden Schwingkreises, die vielleicht auch noch eine Rolle spielt.
Danke fuer eine Antwort. (Wegen des allgemeinen Charakters nicht vom Modell gepostet)
Hans-Georg Schirmer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Resonanzfrequenz ermitteln

Per e-mail hat mir Herr Daniel Consales meinen Verdacht der Dipmeter-Falschanzeigen bestaetigt. Wir haben uns darueber hinaus ueber die Probleme von Oszillatorschaltungen mit Anschluss fuer beliebige Schwingkreise und Zaehleranschluss ausgetauscht. Als recht genaue und einfache Methode schlug er alternativ noch die Methode der lose angekoppelten, impulsartigen Ansteuerung des Schwingkreises vor, wobei die gedaempfte Eigenschwingung des Kreises mit dem Oszilloskop beobachtet und gemessen wird.
Soweit die Information fuer die an diesem Thema Interessierten. Herrn Consales sage ich auch an dieser Stelle: Herzlichen Dank fuer die Hilfestellung.
Hans-Georg Schirmer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Griddipper und Resonanzkurven von Bandfiltern

Nähert man die Spule eines Griddipmeters einem Schwingkreis, bilden die Schwingkreise von a) des Griddippers und b) des zu messenden Resonanzkreises de facto zusammen ein Bandfilter.
Von Bandfiltern ist bekannt, daß die Resonanzkurven bei zu fester Kopplung zweihöckrig werden können. Zu feste Kopplung ensteht bei der Messung mit dem Griddipper, wenn die beiden Spulen zu eng genähert werden.
Beim Bandfilter interessieren i.a. die Übertragungskurven zwischen primärer und sekundärer Seite. Hier ist es aber anders, weil der Schwingkreis des Griddippers die Primärspule bildet und auch nur an dieser Seite die "Reaktion" gemessen wird. Es interessieren also die primärseitigen Verhältnisse eines Bandfilters. Hierzu findet man z.B. in "F.E. Terman: Radio Engineering, 2nd. ed., McGraw-Hill, 1937" die folgenden Kurven.

Die oberen Kurven zeigen den Strom im Primärkreis und damit den im Kreis des Griddippers, während die unteren Kurven die (bekannteren) Durchlaßkurven eines Bandfilters zeigen, jeweils mit dem Parameter K für den Koppelfaktor versehen. (Für die Kurven ist gleiche Güte beider Kreise angenommen.)
Aus den oberen Kurven erkennt man, daß die Kopplung extrem lose sein muß (K < 0,005), damit primärseitig keine doppelten Höcker entstehen. Also den Griddipper sehr lose ankoppeln. Der primäre Strom (also im Schwingkreis des Griddippers) ist ein Maß für die auf den unbekannten Kreis gekoppelte Leistung. Der Osillator des Griddippers darf nur "schwach" schwingen, damit diese Entnahme von Leistung durch den unbekannten Kreis zu einer Verminderung der Schwingamplitude und damit zu einem (gut sichtbaren) "Dip" führt. Das ist bei Eigenbaugeräten zu beachten.
Ist die Kopplung jedoch zu stark, entstehen 2 primärseitige Höcker und damit "Dips" bei 2 Frequenzen, bzw. der "Dip" ist nicht bei der Resonanzfrequenz des unbekannten Kreises.
Unübersichtlich werden die Verhältnisse dann, wenn die Spule des Griddippers so groß ist, daß in einer zu messenden Schaltung mehrere Resonanzkreise angeregt werden.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Messung Schwingkreis

Hier ein Beispiel für die Messung der Resonanzfrequenz.
Für eine RfID Anwendung soll ein Schwingkreis auf einer Leiterplatte mit einer Resonazfrequenz von 13,56 Mhz realisiert werden.
Die Spule besteht aus 3 Windungen einer Leiterbahn auf einer Platine. Der Parallelkondensator soll 150pF betragen.
Damit die Resonanzfrequenz exakt festgelegt werden kann, wurde ein zweiter Kondensator parallel zum ersten vorgesehen.
Zur Messung stand kein Grid-Dip Meter zur Verfügung, deshalb wurde die Resonanzfrequenz wie folgt gemessen:
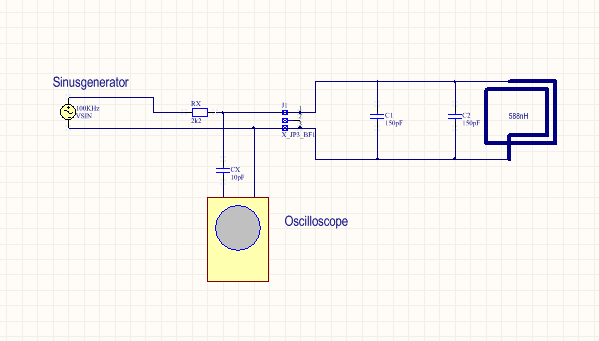
Der Generator mit einer Impedanz von 50 Ohm wurde über einen großen Widerstand ( hier 2,2kOhm ) angeschlossen.
Das Oscilloscope über einen Tastkopf 1Meg/ 15pF und zusätzlich über einen 5pF Kondensator in Reihe.
Dadurch sollte erreicht werden, dass der Schwingkreis durch die Messanordnung möglichst wenig beeinflusst wird.
Die gemessenen Ergebnisse stimmten erstaunlich genau mit den berchneten überein.
Berechnet 13,56Mhz, gemessen 13,8 MHz.
Noch ein Wort zum Tastkopf-Anschluss :
Wenn man den Tastkopf mit der üblichen Kroko-klemme an einem Kabelschwanz anklemmt, werden bei solchen diffizielen Messungen viele störende Signale eingekoppelt. Durch diese Buchse, in welche der Tastkopf eingesteckt wird, werden solche Probleme vermieden.
Heute sind die Bilder nicht so toll !


Georg Beckmann
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Dip Tastkopf

Eine Lösung für einen Dip-Tastkopf, der sich für Wobbelmessungen für Duchlaßkurven von Schwingkreisen eignet, wurde hier vorgestellt.
Seine Schaltung ist recht einfach, aber als Hilfsmittel zum Abgleich von Resonanzkreisen ist der Dip-Tastkopf sehr bequem zu handhaben.
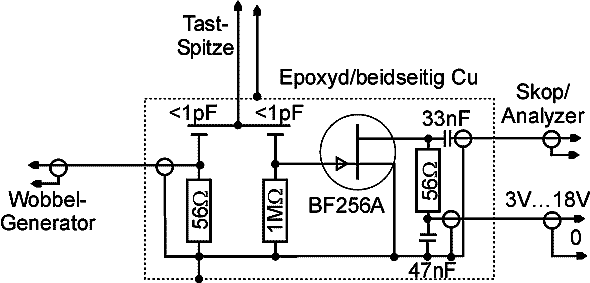
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Messung abklingender Schwingungen

Hallo Herr Schirmer
Zu Post #2:
Ob die Messung der Resonanzfrequenz eines elektrischen Hochfrequenzschwingkreises über die abklingende Schwingung nach einer impulsartigen Anregung messtechnisch so einfach ist würde ich bezweifeln. Der Grund ist das sehr schnelle Abklingen der Schwingung. Kurz zur Theorie dahinter:

Etwas intuitiver als die Abklingkonstante a ist deren Kehrwert 1/a. Dieser gibt die Zeit an, nach der die Amplitude der Schwingung auf 1/e = 0.367... des Anfangswertes zurück gegangen ist. Für die Praxis ist auch die Größe 3/a gut geeignet, nach dieser Zeit ist die Amplitude auf ca. 1/20 des Anfangswertes zurück gegangen.
Nehmen wir als Beispiel einen Schwingkreis im Mittelwellenbereich mit Q=100 und f0=1MHz. Damit ergibt sich 3/a=95µs. Bei einem Schwingkreis im Kurzwellenbereich mit Q=30 und f0=10MHz ist 3/a=2.9µs.
Die gedämpfte Schwingung am Oszilloskop beobachten und messen heist in diesem Fall: Den Vorgang mit Hilfe eines digitalen Speicheroszilloskopes, das vom Impulsgenerator der die Anregung des Schwingkreises vornimmt getriggert wird aufzeichnen und dann ausmessen.
Gruß Jochen Bauer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Messung abklingender Schwingungen

Hallo Herr Bauer,
vielen Dank fuer Ihren Beitrag.
Ich verfuege nur ueber einen bescheidenen Messgeraetebestand und konnte z.B. mangels eines Funktionsgenerators fuer die impulsartige Ansteuerung, die Herr Consales vorschlug, nur einen 2-Transistor Signalinjektor (Multivibrator) verwenden. Es genuegte, um auf dem Bildschirm eines Oszilloskops ein stehendes Bild der gedaempften Schwingung darzustellen. Die Methode scheidet fuer mich allerdings aus einem anderen Grund aus: Mein einfaches analoges Oszilloskop bildet schon Frequenzen ueber 1 MHz kaum noch sichtbar - und ohne das Zimmer zu verdunkeln - ab.
Gruss, Hans-Georg Schirmer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Triggerung

Hallo Herr Schirmer
An die periodische Anregung hatte ich auch schon gedacht. Allerdings hätte ich nicht gedacht, dass sich ohne externe Triggerung des Oszilloskopes ein sauber stehendes Bild produzieren lässt!
Interessehalber: Welche Frequenz hat der Multivibrator und welche Resonanzfrequenz hat der Schwingkreis? Wie ist der Multivibrator angekoppelt?
Gruß Jochen Bauer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Triggerung

Hallo Herr Bauer,
die Triggerung war kein Problem, da der Beginn der "angestossenen" Schwingung ja mit der steilen Flanke des Multivibrators zusammenfiel. Frequenz des Multivibrators ca. 1 kHz, Resonanzfrequenz des Schwingkreises ca. 1 MHz, Kreiskapazitaet 100 pF, lose angekoppelt ueber 10 pF.
Freundliche Gruesse
Hans-Georg Schirmer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Helligkeit des Oszilloskopbildes

Hallo Herr Schirmer
Wahrscheinlich können sie durch Erhöhung der Frequenz des Multivibrators das Schirmbild heller machen. Dazu folgende Überlegung:
Bei einer Frequenz des Schwingkreises von 1MHz und einer angenommenen Güte von Q=100 ist die Zeitspanne in der die Schwingungsamplitude auf 1/20 ihres Anfangswertes abklingt ca. 100µs. Siehe Post #6. Wenn also die Zeitablenkung am Oszilloskop so eingestellt ist, das dieser Abklingvorgang auf der Schirmbreite dargestellt wird, dann zeichnet der Elektronenstrahl innerhalb von 100µs das entsprechende Bild auf der Leuchtschicht. Danach muss für den nächsten Durchlauf (Triggerung) aber wieder auf die erneute Anregung des Schwingkreises gewartet werden. Bei einer Multivibratorfrequenz von 1kHz dauert das dann aber noch 500µs-100µs=400µs. Wobei angenommen wurde, dass die Anregung sowohl mit der fallenden Flanke als auch mit der ansteigenden Flanke erfolgt, deswegen 500µs und nicht 1000µs.
Folglich ist das Verhältnis der Zeitspanne in der die Leuchtschicht durch den Elektronenstrahl angeregt wird zu der Zeitspanne in der diese nachleuchten muss 1/4.
Erhöht man nun die Frequenz des Multivibrators auf z.B. 2.5kHz, so ist die Wartezeit (Dunkelzeit) zwischen zwei Durchläufen nur noch 200µs-100µs=100µs. Nun ist das Verhältnis der Zeitspanne in der die Leuchtschicht durch den Elektronenstrahl angeregt wird zu der Zeitspanne in der diese nachleuchten muss immerhin schon 1/1.
Die Grenze der Erhöhung der Frequenz des Multivibrators liegt natürlich darin, dass die vorausgegangene Schwingung hinreichend abgeklungen sein muss, damit es nicht zu nennenswerten Überlagerungen mit der nachfolgenden Schwingung kommt.
Gruß Jochen Bauer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Oszilloskop
Hallo Herr Schirmer
ich kann Ihnen zwar für das konkrete Problem nicht weiterhelfen aber im Bezug zum "langsamen" Oszilloskop vielleicht weiter helfen.
Ein PM3050 steht hier unbenutzt herum und gerne können Sie das Gerät haben. Leider hat mein Gerät (siehe Link Bilder) einen ziemlichen Gehäuseschaden (unten rechts). Dies tut aber dem Betrieb des Gerätes keinen Abbruch.
Vielleicht kennen Sie einen Pendler, der ab und an in Schweiz ist?
herzliche Grüsse
Pius
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Das geht noch einfacher
Das Problem läßt sich ganz elegant umschiffen, wenn man ein Ozilloskop hat, das einen X-Ausgang hat. Die Rücklaufflanke dieser Spannung ist ideal geeignet, um einen Schwingkreis anzustoßen, und obendrein ist das resultierende Signal automatisch synchron. Man koppelt den Ausgang über einige pF und einen Trennwiderstand von 10 kOhm (bzw. mehr oder weniger, je nach Frequenz) an den Kreis, schaltet den Trigger auf freilaufend und braucht dann nur noch die Kurve passend strecken. Da sofort nach dem Durchlauf neu getriggert wird, gibt's auch kein Problem mit der Helligkeit mehr. Funktioniert mit meinem Voltcraft-Oskar hervorzüglich. Der Vorschlag stammt aus einem der alten Bastelbücher.
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.