Spiegelfrequenz-Unterdrückung

Beim Empfang mit einem Superhet (Super) wird das Empfangssignal in die Zwischenfrequenz-Ebene umgesetzt, weil sich auf dieser ZF die für die Selektion erforderlichen Filter besser realisieren lassen.

Über die Auswahl der ZF-Frequenzen und die damit zusammen hängenden Problemstellungen findet man eine Abhandlung unter "Texte".

Hier soll nun das dort ebenfalls angesprochene Problem des Spiegel-Empfangs unter Aspekten der schaltungstechnischen Realisieung der gewünschten "Spiegelfrequenz-Unterdrückung" betrachtet werden.

Bekanntlich wird bei einem Mischvorgang sowohl ein Signal, das um die ZF-Frequenz unterhalb der Frequenz des Oszillator-Signals liegt, als auch eines, das um die ZF-Frequenz darüber liegt, auf die ZF-Frequenz umgesetzt.

Die Grafik zeigt prinzipiell diese Umsetzung, einschließlich durch farbige Pfeile, wie die in die ZF-Ebene umgesetzten Spektren "wandern", wenn die  Abstimmung (d.h. die Frequenz des Oszillators) verändert wird.

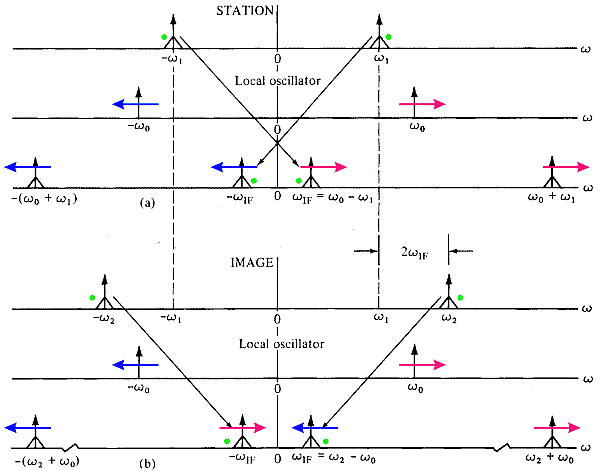
Durch diese Eigenschaft der Frequenzumsetzung (in einem Mischer) würde man also gleichzeitig 2 unterschiedliche Sender empfangen, was nicht erwünscht ist. Dieses Problem behebt man mit Hilfe (mindestens) einer passend abgestimmten Vorselektion (Preselection).

Eine Vorselektion, die, wie gezeicnet, (praktisch) außer dem gewünschten Sender nichts weiter "durch läßt" gibt es nicht. Mit erträglichem Aufwand, z.B. durch ein (abgestimmten) Eingangs-Bandfilter (also mit dreifach-Drehko) erreicht man im Prinzip eine ausreichende Unterdrückung des Spiegel-Signals (Image Attenuation).

Die Durchlaßkurve der Eingangs-Selektion ist hier mit |H₁(f)| bezeichnet.

Nun ist die Verwendung eines dreifach-Drehkos vergleichsweise aufwendig (und teuer). In der Praxis wurden daher auch andere (nicht ganz so wirkungsvolle) Methoden angewendet, um die Spiegelfrequenz zu unterdrücken.

In der Literatur ist zu diesem Thema selten etwas zu finden. Ausnahmen hiervon bilden z.B.:

Sturley, K.R.: Radio Receiver Design, Part 1, 2nd ed., Chapman & Hall, 1953
Zepler, E.E.: The Technique of Radio Design, 3rd. imp., Chapman & Hall, 1945
Terman, F.E.: Radio Engineering, 2nd. ed., Mc-Graw-Hill, 1937

Der "Trick" bei diesen Lösungen besteht praktisch immer darin, die Koppel-Induktivitäten der verschiedenen hierbei verwendeten Spulen im Zusammenspiel mit Koppel-Kondensatoren so zu dimensionieren, daß sich im Bereich der Spiegelfrequenzen (mindestens) ein Notch (Sperrlücke) bildet.

Die Berechnungen hierzu sind ziemlich "formel-lastig". Zur Dimensionierung sei daher auf die Literaturstellen verwiesen. Hier wird "nur" die prinzipielle Funktionsweise betrachtet.

Im einfachsten Fall wird ein Serien-Sperrkreis im Eingang verwendet, dessen Induktivität mit derjenigen des Eingangskreises verkoppelt ist (Koppelinduktivität M)  Im Ersatzschaltbild sieht das so aus.

Man erhält damit eine gute Sperrdämpfung für eine Frequenz.

Daneben ist die Unterdrückung der Spiegelfrequenz nicht mehr so gut, aber trotzdem noch besser, als nur mit einem abgestimmten Vorkreis alleine. Da die Güten der Schwingkreise für die oberen Mittelwellen geringer sind als für die unteren Mittelwellen, wird das Maximum der hier zusätzlich erreichbaren Sperrdämpfung zu den höheren Frequenzen hin gelegt.

In der Praxis der Empfänger gibt es mehrere Schaltungsvarianten, die wegen der zahlreichen Verkopplungen kompliziert erscheinen. 

In diesem Beispiel gibt es 2 Verkopplungen. Die Gleichung rechts ist das Ergebnis einer Berechnung.

Das ist offensichtlich das gleiche Prinzip aus der anderen Literaturstelle.

Hier sind ebenfalls zwei Verkopplungen, aber unterschiedlich zu den vorherigen.

Dies ist ein Beispiel für 3 Verkopplungen. Damit lassen sich für 2 Frequenzen zusätzliche Sperrdämpfungen realisieren. Das gibt insgesamt eine bessere Spiegelfrequenzunterdrückung.

Hier noch eine Variante zur vorhergehenden Anordnung, bei der noch ein Resonanzkreis L₀C₀ geignet dimensioniert werden muß.

Diese Methode wird z.B. bei Kurzwelle angewendet. Hierbei entsteht die Sperrdämpfung im Zusammenspiel von M und C₅. In einer praktischen Schaltung ist C₅ ein Trimmer.

Dies ist eine weitere bei Kurzwellen angewendete Variante, hier zwischen der Vorröhre (R.F.) und der Mischröhre (F.C.).

Bei Radioempfängern findet man entsprechende Schaltungen zur Unterdrückung des Spiegel-Empfangs z.B. in Geräten von Philips. Ein Beispiel hierzu ist der Philips 789A, von dem ein Schaltungsauszug hier zu sehen ist.

Wenn man den Signalweg hier verfolgt, erkennt man, daß z.B. für Mittelwelle zwischen Antenne und Steuergitter der Mischröhre mehrere Wege bestehen. Dadurch entstehen Kompensationen, die im Frequenzgang der Eingangsschaltung zu den (gewünschten) Zusatzdämpfungen für den Spiegelfrequenzbereich führen. Wenn in diesem Teil (keramische) Kondensatoren zu ersetzen sind, tut man gut daran, diese wertemäßig exakt zu ersetzen, weil sich sonst eine Verstimmung des "Brücken-Gleichgewichts" ergibt, wodurch dann die zusätzliche Sperrdämpfung vermindert würde.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Bei Kurzwellen Einfach-Superhet Empfängern gibt es für die Realisierung des Vorkreises im wesentlichen zwei Methoden. Im einfachsten Fall wird, wie beim Mittel- und Langwellenempfang auch, ein Einzelschwingkreis um die Zwischenfrequenz versetzt mit dem Oszillatorkreis mitgeführt. Mit dieser Methode lassen sich auch mehrere KW-Rundfunkbänder (z.B. 49m, 41m, 31m) sowie der dazwischen liegende Frequenzbereich nahtlos überstreichen. Alternativ dazu kann aber auch mit Hilfe eines Wellenschalters der Vor- und Oszillatorkreis zwischen den einzelnen KW-Rundfunkbänder umgeschaltet werden und der Drehkondensator zur Abstimmung innerhalb des gewählten Bandes verwendet werden. Dies ergibt natürlich eine deutlich bessere Auflösung und genauere Einstellmöglichkeit auf der Frequenzskala. Bei den "schmalen" KW-Rundfunkbändern (z.B. 49m von 5.9MHz bis 6.2MHz) kann der mitgeführte Vorkreis durch ein fest abgestimmtes Bandfilter ersetzt werden, welches das gesamte jeweils ausgewählte KW-Rundfunkband durchlässt. Bei den "breiten" KW-Rundfunkbändern (z.B. 19m von 15.1MHz bis 15.8MHz) ist dazu je nach Zwischenfrequenz eventuell eine Unterteilung in zwei Teilbänder notwendig.

Genau wie beim mitgeführten Vorkreis stellt sich auch hier die Aufgabe einer möglichst guten Unterdrückung der Spiegelfrequenz, bzw. des "Spiegelbandes". Wird als Beispiel für das 49m Band ein fest abgestimmtes Bandfilter mit Durchlass des "Empfangsbandes" 5.9MHz bis 6.2MHz verwendet, so muss bei einer Zwischenfrequenz von 450kHz und einer Oszillatorfrequenz überhalb des Empfangsbandes das Spiegelband von 6.8MHz bis 7.1MHz möglichst gut unterdrückt werden. Liegt die Oszillatorfrequenz unterhalb des Empfangsbandes, so liegt das zu unterdrückende Spiegelband von 5.0MHz bis 5.3MHz.

In seinem im vorherigen Post aufgelisteten Buch "Radio Receiver Design" gibt K.R. Sturley eine Methode an, wie die Spiegelbandunterdrückung bei fest abgestimmten Eingangsbandfiltern deutlich verbessert werden kann. Es handelt sich dabei um eine geschickte Anwendung der Mischung aus kapazitiver Scheitelpunkt- und induktiver Kopplung innerhalb des Bandfilters um ein Minimum der Durchlasskurve im Spiegelband zu erzielen. Als Beispiel zeigt Sturley eine bereits im vorherigen Post abgebildete Schaltung bei der das Bandfilter aus einer mit einer Kapazität C₁ und Induktivität L₁ abgestimmten Antenne auf der Primärseite sowie einer Induktivität L₂ und (Trimmer)Kapazität C₂ auf der Sekundärseite besteht. Die Kopplung erfolgt dabei einerseits kapazitiv durch den Kondensator C₅ und andererseits induktiv durch Kopplung der beiden Spulen. Hier nochmals das Schaltbild dazu:

Prinzipiell kann jedes Bandfilter mit einer Mischung aus kapazitiver Scheitelpunkt- und induktiver
Kopplung verwendet werden. Die folgende Abbildung zeigt ein entsprechend "mischgekoppeltes" Bandfilter, das auf der Primärseite von einer Stromquelle (z.B. HF-Vorstufe mit einer Pentode) angetrieben wird. Die Ausgangsspannung auf der Sekundärseite wird der nächsten Stufe zugeführt.

Um die für KW-Rundfunkbänder erforderliche Bandbreite (z.B. 5.9 bis 6.2MHz) zu erreichen ist meistens eine zusätzliche Dämpfung der Schwingkreise mittels den Widerständen R₁ und R₂ erforderlich. Genau genommen addieren sich die Kehrwerte dieser Widerstände zu den Kehrwerten der
Parallelverlustwiderstände in den Schwingkreisen.

Mit etwas Aufwand kann nun eine Formel für die komplexe Ausgangsspannung am Sekundärkreis als Funktion der Antriebsfrequenz hergeleitet werden (der interessierte Leser sei auf das PDF Dokument im Anhang verweisen). Mit Hilfe von Plotting Programmen, die in der Lage sind mit komplexen Zahlen zu arbeiten und insbesondere deren Beträge (Absolutwerte) zu ermitteln, können nun die Durchlasskurven dieses mischgekoppelten Bandfilters für verschiedene Werte der Bauteile und Kopplungsstärken geplottet werden.

Als Beispiel hierfür sei nun ein Eingangsbandfilter für das 49m Band von 5.9MHz bis 6.2MHz betrachtet. Die Zwischenfrequenz sei 450kHz und die Oszillatorfrequenz soll unterhalb der
Empfangsfrequenz liegen. Das zu unterdrückende Spiegelband liegt damit zwischen 5.0MHz und 5.3MHz. Mit Hilfe einer von Sturley angegebenen Formal für die Lage des durch die Mischkopplung erzeugten Minimums der Durchlasskurve und etwas "numerischem Probieren" lassen sich schnell Werte für die Bauteile und Kopplungen in der oben abgebildeten Bandfilterschaltung ermitteln (R₁=R₂=60kΩ, L₁=L₂=39.6µH, C₁=C₂=15pF, C_c=2.87pF und k=0.12), die zu einer Durchlasskurve mit guter Spiegelbandunterdrückung führen, wie an der grünen Kurve im nachfolgenden Plot zu sehen ist:

Zum Vergleich wurde noch eine Durchlasskurve mit praktisch rein kapazitiver Scheitelpunktkopplung
(C_c=0.65pF, k=10^-6, L₁=L₂=44.3µH, sonstige Werte wie vorher, rote Kurve) sowie eine Durchlasskurve
mit praktisch rein induktiver Kopplung ( C_c=1fF, k=0.0415, L₁=L₂=46.2µF, sonstige Werte wie vorher, blaue Kurve) in das selbe Diagramm geplottet. Noch deutlicher wird die Verbesserung der Spiegelbandunterdrückung durch den Übergang von der linearen Spannungsskala zur logarithmischen Leistungs-Dezibelskala, wie im folgenden Plot getan:

 

Anlagen:

• Formeln Bandfilter mit Mischkopplung (98 KB)

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Nach der in Post #2 erfolgten theoretischen Beschreibung des mischgekoppelten KW-Eingangsbandfilters mit Spiegelbandunterdrückung soll hier nun eine praktische Realisierung eines derartigen Filters erfolgen und Messungen daran vorgenommen werden.

Zunächst stellt sich dabei die Frage, wie schwierig die praktische Umsetzung von Konstruktion und Abgleich ist. Immerhin müssen ja die Bauteile so dimensioniert werden, dass die Frequenzkurve des Bandfilters sowohl im Durchlassbereich die gewünschte Form (Doppelhöcker mit "center dip" max. -3dB) und Mittenfrequenz hat und gleichzeitig das Minimum zur verbesserten Spiegelbandunterdrückung an der richtigen Stelle auf der Frequenzskala zu liegen kommt. Außerdem soll die Form und Position des Doppelhöckers sowie die Position des Minimums zur verbesserten Spiegelbandunterdrückung möglichst unabhängig von den parasitären Kapazitäten des mechanischen Aufbaus sein.

Um es vorweg zu nehmen: Mit Hilfe der theoretischen Analyse dieses KW-Eingangsbandfilters und dem daraus gewonnenen Verständnis lassen sich solche Bandfilter problemlos auch im "Hobbylabor" aufbauen.

Wir gehen aus von den Voraussetzungen in Post #2, nehmen also an, dass die Oszillatorfrequenz unterhalb der Empfangsfrequenz liegt. Das zu unterdrückende Spiegelband liegt damit um die doppelte Zwischenfrequenz unterhalb des Empfangsbandes. Um hier ein weiteres Minimum der Durchlasskurve zu erreichen muss folgende Voraussetzung erfüllt sein: Die induktive Kopplung der Spulen muss der kapazitiven Scheitelpunktkopplung entgegen gerichtet sein, dabei muss die kapazitive Scheitelpunktkopplung aber überwiegen. In anderen Worten: Die überkritische Kopplung und die daraus resultierende Doppelhöckerkurve wird durch eine hinreichend starke kapazitive Scheitelpunktkopplung, reduziert durch eine entsprechend schwächere induktive Kopplung erreicht. Dies ist daran zu sehen, dass eine Erhöhung der induktiven Kopplung die effektive Kopplungsstärke vermindert (weniger ausgeprägter Doppelhöcker) und umgekehrt.

Wird nun die induktive Kopplung relativ stark gemacht, so kann und muss der Scheitelpunktkondensator entsprechend groß sein um die gewünschte überkritische effektive Kopplung zu erreichen. Der Scheitelpunktkondensator kann somit problemlos in den Wertebereich von z.B. 6-12pF geschoben werden und damit ist der Aufbau natürlich deutlich weniger gegenüber kleinen parasitären Kopplungskapazitäten oder auch der Handkapazität des Experimentators anfällig.

Das nächste sich stellende Problem ist die Einstellung der induktiven Kopplung und zwar möglichst
unabhängig von der Einstellung der Induktivität der Spulen über Ferritkernschrauben. Dies würde
zunächst eine aufwendige Mechanik zur Veränderung des Spulenabstandes erfordern. Bei den meisten ZF-Bandfiltern wurde der Abstand der Spulen experimentell ermittelt und danach mit diesem festen Abstand in die Serienfertigung gegangen, mit den Ferritkernschrauben können dann beim Abgleich nur Induktivität und Kopplungsfaktor gleichzeitig beeinflusst werden. Die Lösung dieses Problems im Rahmen einer "hobbymäßigen" Einzelanfertigung ist folgende: Damit, wie erforderlich, die induktive Kopplung der kapazitiven Scheitelpunktkopplung entgegen gerichtet ist, muss der Kopplungsfaktor der beiden Spulen positiv sein, d.h. der Windungssinn muss gleich sein. In diesem Fall kann die Kopplung der Spulen aber auch über eine gemeinsame Fußpunktinduktivität erfolgen (siehe Diagramm weiter unten), also etwas salopp ausgedrückt: Eine induktive Kopplung nach dem galvanisch nicht getrennten Spartrafo Prinzip.

Die Stärke der induktiven Kopplung kann nun durch Veränderung der Größe der Fußpunktinduktivität mittels Ferritkernschraube eingestellt werden. Die sich dadurch ergebende Veränderung der Gesamtinduktivität in den beiden Kreisen des Bandfilters kann leicht durch eine entsprechende Veränderung der Induktivität der Hauptspulen (ebenfalls durch Ferritkernschrauben) kompensiert werden. Damit können nun auch einfach erhältliche, abgleichbare "Mini-Spulen" verwendet werden und das selbst wickeln entfällt.

Die Ankopplung des Signalgenerators mit einem 50Ω Ausgang geschieht über den Widerstand R, der
damit gleichzeitig als Parallelverlustwiderstand die zusätzliche Dämpfung des Bandfilters bestimmt.

Die Ankopplung des Oszilloskoptastkopfes erfolgt über einen sehr großen kapazitiven Spannungsteiler um die Auswirkung der Tastkopf- und Eingangskapazität des Oszilloskops gering zu halten. Der Schwingkreiskondensator des Sekundärkreises mit typischerweise 10-100pF bildet dabei den einen Kondensator des Spannungsteilers. Der Kondensator, an dem der Tastkopf (dieser kann nun sogar ein 1:1 Tastkopf sein) angeschlossen wird hat in der vorliegenden Schaltung eine Kapazität von 1.5nF, die HF-Drossel von 33mH parallel dazu schließt vom Tastkopf eingefangene Netzbrummstörungen kurz und sorgt für ein ruhiges Oszilloskopbild auch bei maximaler Vertikalverstärkung.

Es ergibt sich damit folgende Schaltung,

die auf dem Steckbrett aufgebaut wurde:

Als Beispiel sei nun ein KW-Eingangsbandfilter für das 75m Rundfunkband von 3900kHz bis 4000kHz
angegeben. Obwohl das 75m Rundfunkband bei 4000kHz endet, finden sich gelegentlich auch Radiostationen etwas darüber. Wir legen daher 3890kHz bis 4060kHz als -3dB Soll-Durchlassbereich des Filters fest. Bei einer ZF von 450kHz und der Oszillatorfrequenz unterhalb der Empfangsfrequenz ergibt sich damit ein Spiegelband von 2990kHz bis 3160kHz das durch geeignete Platzierung des durch die Mischkopplung zusätzlichen in der Durchlasskurve entstehenden Minimums möglichst gut unterdrückt werden soll.

Die notwendigen Werte der Bauteile liegen grob bei: C₁=C₂=47pF, L₁=L₂=35µH, L_c=3.5µH, C_c=6.8pF und R=56kΩ. Das folgende Bild zeigt die Durchlasskurve dieses Bandfilters:

Die Mittenfrequenz ist im obigen Bild auf 3970kHz eingestellt, die Frequenzskala ist 100kHz/div. Es
ist sehr deutlich der schnellere Abfall zu niedrigeren Frequenzen (also zum Spiegelband) hin zu sehen.
Um den Bereich des Spiegelbandes auf den Schirm zu bekommen, muss die Frequenzskala auf 300kHz/div zusammengestaucht werden:

Die Kurve ist im Bereich des Spiegelbandes nicht mehr von einer Nullinie zu unterscheiden. Eine
Erhöhung der Vertikalverstärkung auf deren Maximalwert unter Beibehaltung von Frequenzskala und
Mittenfrequenz zeigt jedoch deutlich das theoretisch vorhergesagte Minimum:

Das Minimum wurde hier, damit es besser zu erkennen ist, etwas rechts des Spiegelbandes auf ca.
3250kHz gelegt. Wird das Minimum weiter zu niedrigen Frequenzen hin in das Spiegelband hinein
geschoben, so ist es im Rauschen der Messanordnung nur schwer zu erkennen.

Um Rückblickend auf das Problem der richtigen Platzierung des zusätzlichen Minimums bei
gleichzeitigem Erreichen der vorgegebenen Doppelhöckerkurve zurück zu kommen: Es zeigt sich, dass durch durchprobieren verschiedener Werte aus der Normreihe für den Kondensator zur
Scheitelpunktkopplung (4.7pF, 6.8pF, 8.2pF, ...) schnell ein Wert gefunden werden kann, bei dem beides in guter Näherung erreicht werden kann. Ein Feinabgleich kann dann bei Bedarf mit einem Trimmer parallel zum Scheitelpunktkondensator vorgenommen werden.

 

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Eine interessante Art der Unterdrückung von Spiegelfrequenzen erfolgt bei einem Mittelwellen-Radio von  RCA Victor Co.: 4-X-641 Driscll.  Hier dient der fest abgestimmte Primärkreis des (abstimmbaren) HF-Filters zwischen der 12BA6 und der 12BE6 im Zusammenwirken mit Streuinduktivitäten und einem 2,2pF Kondensator (C4; Stirnpunkt-Kopplung) diesem Zweck.

Dies verblüfft um so mehr, als Stirnpunkt-Kopplung "normalerweise" in Bezug auf Spiegelfrequenz-Unterdrückung ungünstig ist.

Joe Sousa hat die Funktionsweise analysiert und mit LT-Spice simuliert. Dieser Thread ist auf Englisch unter "rca: RF Transformer analysis" zu finden.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Im Zusammenhang mit fest abgestimmten Eingangsbandfiltern in KW-Empfängern anstelle eines im Abstand der Zwischenfrequenz mit der Oszillatorfrequenz mitgeführten Einzelkreises stellt sich natürlich sofort die Frage ob der mitgeführte Einzelkreis eine bessere Unterdrückung der Spiegelfrequenz ermöglicht. Zunächst könnte man sicherlich der Meinung sein, dass ein für das jeweils zu empfangende KW-Band fest abgestimmtes Eingangsbandfilter lediglich eine einfachere und damit billigere Lösung auf Kosten der Spiegelfrequenzunterdrückung darstellt.

Es zeigt sich allerdings schnell, dass bei den schmalen KW-Bändern (300kHz) ein mitgeführter Einzelkreis gegenüber einem fest abgestimmten Eingangsbandfilter ohne Mischkopplungs-Notch im Spiegelfrequenzband keine verbesserte Unterdrückung der Spiegelfrequenz liefert. Wird ein fest abgestimmtes Eingangsbandfilter mit Mischkopplungs-Notch im Spiegelfrequenzband verwendet, so ist dieses dem mitgeführten Einzelkreis bei der Spiegelfrequenzunterdrückung sogar deutlich überlegen.

Betrachten wir dazu nochmals das Diagramm der Resonanzkurven für die verschiedenen Bandfilter aus Post #2 und normieren die maximale Ausgangsspannung auf 1V. Nun lassen sich die Resonanzkurven direkt mit der Resonanzkurve eines Einzelkreises vergleichen. Der Einzelkreis hat im vorliegenden Falle, in dem die Oszillatorfrequenz unter der Empfangsfrequenz liegt, seinen größten Vorteil gegenüber dem fest abgestimmten Bandfilter am oberen Ende des Empfangsbandes. Wir plotten daher die Resonanzkurve eines Einzelkreises mit einem Gütefaktor von Q=88 (was in diesem Frequenzbereich schon ein recht guter Wert ist) bei einer Resonanzfrequenz von ca. 6.2MHz (L=44µH, C=15pF und R=150kΩ) zusammen mit den Resonanzkurven der verschiedenen Bandfiltervarianten aus Post #2.

Offensichtlich liefert der Einzelkreis, wie bereits erwähnt, selbst an dem Ende des Empfangsbandes an dem er seinen größten Vorteil gegenüber dem fest abgestimmten Bandfilter hat keine verbesserte Spiegelfrequenzunterdrückung. Einem fest abgestimmten Eingangsbandfilter mit Notch im Spiegelfrequenzband ist der Einzelkreis, wie ebenfalls bereits erwähnt, offensichtlich sogar deutlich unterlegen. Der Vorteil des Einzelkreises liegt hauptsächlich in der höheren absoluten Ausgangsspannung gegenüber dem Bandfilter, was bei einem Superhet mit entsprechend
leistungsfähigem ZF-Verstärker allerdings weniger relevant als eine gute Spiegelfrequenzunterdrückung ist.

 

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.