Warum kann ein Radio mit einem Schwingkreis Sender trennen?
Warum kann ein Radio mit einem Schwingkreis Sender trennen?

Meine im Radiomuseum unter "TEXTE" veröffentlichte Reihe von Messungen an KW -Vorsatzteilen (Adapter) hat ein gerne und allzu leicht übersehenes Problem aufgezeigt.
Warum oder wie trennt ein Audion mit nur einem Schwingkreis, aber mit Rückopplung, überhaupt Sender im KW Bereich?
Rein aus der Sicht des Technikers ein nicht ganz einfach zu beschreibendes Phänomen.
Die umfangreiche Literatur arbeitet da mit Formeln, Diagrammen und Kurven in grösserer Zahl.
Andererseits, herrscht eine allgemeine Meinung vor, die ich hier versuche zu widerlegen, bzw. aufzuarbeiten.
Ganz ohne Diskurs wird das wohl nicht gehen.
Man sagt und liest allgemein: Mit der Rückopplung wird der Kreis entdämpft und damit die Trennschärfe erhöht.
Woran ist das zu erkennen?
Wenn das so ist, muss ein rückgekoppelbares Audion, wenn es auf eine Frequenz neben einem Sender abgestimmt ist, doch folgendes zeigen:
Ø Fakt 1
Ohne Rückopplung, also wenn der Kreis nicht entdämpft wird, kann ich den Sender vom Nachbarkanal hören.
Das ist auch so und kann leicht überprüft werden.
Ziehe ich jetzt die Rückopplung an, soll ja nach landläufiger Meinung die Bandbreite des Abstimmkreises kleiner werden.
Wenn es so ist, dass die (in diesem speziellen Fall ohne Nutzsender) Bandbreite durch die Rückopplung verkleinert wird, müsste ja der Sender vom Nachbarkanal zumindest leiser werden. Sehen Sie nach und Sie werden beobachten, es ist nicht so. Nichts tut sich, gar nichts.
Als erste Aussage halte ich fest: der Nachbarsender wird in dem Falle wenn kein Nutz -Sender empfangen wird, mit der Rückopplung nicht abgeschwächt. Ich kann mit der Rückopplung die wirksame Trennschärfe zum Nachbarsender hin also nicht erhöhen.
Ø Fakt 2
Für den Fall, der ja praktisch der Normalfall ist, wenn ein Sender gehört wird und der Nachbarsender noch durchschlägt, kann ich aber den Lautstärkeeindruck zwischen den beiden Sendern verändern. Auch leicht zu überprüfen. Nutzsender und Empfänger sind aufeinander abgestimmt, mit der Rückopplung kann das Verhältnis Nutz -Störsender geändert werden.
Als zweite Aussage: halte ich fest: mit der Rückopplung kann der tatsächliche Lautstärkeunterschied zwischen Nutz und Stör -Sender sehr wohl verändert werden. Das ist nun aber ein Beweis dafür, dass sich die (wirksame bzw subjektive) Trennschärfe verändert haben muss.
Somit stehen zwei Behauptungen nebeneinander. In einem Falle (a) ändert die Rückopplung nichts an der Trennschärfe, im Fall (b) aber wohl, ( Fachjargon: Zweizeichen -Selektion).
Wie geht das zusammen?
Ab hier wird es nicht ganz leicht der Beweislage zu folgen.
Ø Fakt Nr. 3
Die Rückopplung entdämpft nämlich nicht den Schwingkreis als solchen, sondern sie hebt das Signal welches am Eingang der rückgekoppelten Stufe, hier das Audion, um den Betrag des Faktors der Rückopplung an.
Zum Beispiel: 1zu 10 oder 15, wie es in meinen Messungen zu den VE's angegeben wird.
Diese Anhebung passiert nur dann, wenn das Eingangssignal und die Rückopplung in Phase (gleichphasig) sind.
Dieser Fall tritt aber nur dann ein, wenn der Schwingkreis genau auf der Frequenz steht die gehört wird und auf die auch rückgekoppelt wird.
Denn das rückgekoppelte Signal ist nur dann in Phase mit der Nutzfrequenz, wenn der Abstimmkreis auf der richtigen Empfangsfrequenz steht. Nur dann wird das Signal angehoben und sichert einen Abstand zum Störsender.
Warum ist das so?
Jeder Schwingkreis ändert dann, wird er über einen Frequenzbereich dargestellt, nicht nur die Amplitude, sondern auch die Phase. Allgemein gilt: unterhalb seiner Resonanzfrequenz wirkt er induktiv, oberhalb kapazitiv und bei Resonanz reell also wie ein Ohmscher Widerstand.
Die Phase geht in der Mitte durch Null, er wirkt dort wie ein ohmscher Widerstand.
Dieses Bild zeigt normiert, d. h. ohne Dimensionen den Verlauf von Impedanz ( Wechselstrom widerstand) und Phase eines Einzelkreises.
Die Bandbreite eines Kreises wird bei -3db Abfall der Impedanz entspricht einer Phasenabweichung von 45 ° angegeben. Dies kurve gilt auch für die Rückopplung.
Bild 1
Von der Anode des Audions wird über eine um 180° gedrehte Wicklung das Verstärkte Eingangssignal dosiert zurückgeführt.
Die beiden Signale ( Ursignal und rückgekoppeltes) addieren sich nur dann, wenn der Schwingkreis reell wirkt, also exakt bei der Nutzfrequenz
Das kann man leicht überprüfen.
Sender und Empfänger aufeinander abstimmen. Die Rückopplung von Null bis Max. (dort wo es pfeift, weil das Audion schwingt) anziehen. Der Nutzsender wird ganz erheblich in seiner Lautstärke geändert.
Jetzt verstimme man den Empfänger oder den Messender etwas zur Seite, der Sender ist immer noch hörbar aber, die Lautstärke kann nicht mehr geändert werden und am Ende pfeift es wieder, weil das Audion schwingt.
Ø Fakt Nr.4
Das ist ein weiterer Beleg dafür nicht der Schwingkreis wird mit der Rückopplung beeinflusst, sondern sie hebt das Signal welches am Eingang der Rückgekoppelten Stufe, hier das Audion, entsprechend dem Rückopplungsfaktor an.
Weil damit aber andere Frequenzen ( benachbarte), nicht angehoben werden, dal diese nicht in Phase mit dem Rückopplungssignal sind, wird nun tatsächlich die wirksame Trennschärfe geändert.
Wir halten fest: nur Signale bei denen die Phasenlage zwischen Eingangs- und Rückopplungs - Signal in Phase sind, werden bevorzugt ( verstärkt) im Fall des Audions demoduliert. Das ist immer dann der Fall, Sender und Empfänger sind exakt auf einander abgestimmt. Alle anderen Frequenzen werden zwar auch demoduliert, aber um den Faktor der Rückopplung schwächer.
Das beweist nun eindeutig die Trennschärfe hat sich hörbar geändert. Am Schwingkreis als solches, hat sich aber nichts verändert.
Das kommt nun daher, dass jede Betrachtung oder Definition eines Kreises danach erfolgt, wie sich an ihm Spannung, Strom und Phase benehmen.
Wird nun mit der Rückopplung das Verhalten dieser drei Grössen beeinflusst, habe ich auch technisch gesehen den Kreis geändert. Aber nur bei Übereinstimmung der Phasenlagen, also in einem schmalen Bereich um die Mittenfrequenz. Von einer Rückopplung mit der ein Signal angehoben wird, kann man nur dann sprechen, wenn die Phasenlagen übereinstimmen also bei Resonanz.
Ohne ein Signal, wird jede Stufe wird sie vom Ausgang zum Eingang rückgekoppelt, solange mehr entdämpft bis die Stufe ins Schwingen (selbsterregung) gerät. Sie wird also zum Oszillator. Sonst nichts.
Fakt 5
Wenn nun aber die Anhebung des Nutzsenders mittels Rückopplung wie gezeigt mit der Phasenlage beeinflussbar ist, geht das auch bei Kurzwelle. Weil auch dort die Phasenlage über die Resonanzkurve gesehen nur bei der Mittenfrequenz mit der Rückopplung übereinstimmt, habe ich dort die gleichen theoretischen Verhältnisse wie bei Mittelwelle. Es ist lediglich eine weit grösser Frequenzänderung des Kreises nötig. Ob ich einen Sender anheben kann oder nicht, hängt nur davon ab, stimmt die Abstimmung des Empfängers mit der Senderfrequenz überein oder nicht?
Unberührt von alldem, bleibt eines, ist der Störsender so stark, dass er in die Grössenordnung des mit der Rückopplung angehobenen Signals vom Nutzsender kommt, schlägt der natürlich voll auf den Nutzsender durch. Da hilft dann nur noch ein Sperrkreis für den Störer.
Dieser ganzen Problematik kommt noch eine Tatsache entgegen.
Weil, das Audion wie jeder andere Signalgleichrichter auch, eine Schwelle hat, unterhalb der ein Signal nicht erkannt also demoduliert wird, kommt es zu einer ungewollten oder zufälligen Auswahl von Sendern.
Der Abstand von Nutz- zu Störsender wird dabei speziell bei KW, mit den sehr unterschiedlichen Feldstärken der Sender, um einiges vergrössert. Die schwachen dazwischen fallen einfach unter den Tisch. Liegen zwei starke Sender zu dicht beieinander, sind die mit allen Tricks nicht auseinander zu halten.
Es gibt da zwar noch einen Effekt den das Audion im Falle eines starken Störsenders bei schwachem Nutzsender bereithält, der Störsender wird zu einem gewissen Teil von der Gleichrichterschaltung unterdrückt, das würde uns aber in die totale Mathematik und Theorie hinein führen.
Wer will kann ja den Versuch mit einem fixen und einem Variablen Sender machen. Abhängig von den Feldstärken und Frequenzabständen zeigt sich, dass der Störsender durch die Schaltung mit Rückkopplung abgeschwächt wird.
Es muss dazu die Frequenz und Signalstärke des Störsenders verändert und natürlich die Rückopplung feinfühlig bedient werden.
Es wird tatsächlich der Störer im hohen Masse unterdrückt.
Hat man, wie ich, zwei Messender zur Verfügung kann man die Modulationen zu und abschalten und hat damit eine Kontrolle wen höre ich?
Da kommt erstaunliches zum Vorschein. Mit all' diesen Effekten, ist es mit fixen Fingern auch möglich KW zu hören.
Bleibt am Schluss noch der Trägerschwund.
Dagegen ist beim Audion kein Kraut gewachsen. Will heissen: es kommt wie es kommt. Mal laut mal leise oder gar nicht (die Schwelle des Gleichrichters)
Schlussbemerkung:
Ein durchschnittlicher 6Kreis- Super hat bei +/- 9 kHz Verstimmung eine Trennschärfe von 1:50 bis 1: 100 je nach Aufwand und (vor)eingestellter Bandbreite.
Bei einem VE 301Wdyn habe ich folgende Werte der Trennschärfe ohne jegliche Rückopplung gemessen:
Bei 600 kHz im Abstand von 9 kHz= 1:2, bei 18 kHz= 1:4 und bei 27 kHz= 1:5,6.
Bei 170khz im Abstand von 9 kHz = 1:4,5, bei 18 kHz= 1:8,0 und bei 27kHz= 1:11,5
Bei KW mit dem KW Vorsatz ELTEWE 104
Bei 6500khz im Abstand von 50kHz= 1:1,6 und bei 100kHz= 1:2,5
Bei 14.000 kHz im Abstand von 50kHz= 1.1,06 und bei 100kHz 1: 1,25.
Man kann daraus leicht ersehen, dass mit einem Einkreiser, sowohl bei MW und LW und erst recht bei KW, aufgrund der Kreisdaten ohne Rückopplung, der Empfang von Nachbarsendern praktisch unmöglich ist wenn sie unterschiedliche Signalstärken aufweisen.
Nur die dabei nützliche veränderliche Antennenankopplung, sowie das Phänomen der Rückopplung wie oben beschrieben machen es möglich, dass es überhaupt funktioniert in der Praxis.
Die Geschicklichkeit des Operators ist dabei mindestens genau so wichtig.
Wenn Sie überlegen, was mit einer Rückopplung vom Faktor 10 bis 15 oder gar 20, möglich ist, kommt man auf erstaunliche Werte auch beim Einkreiser.
Hans M. Knoll
18.September 2004
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Audion mit pos. Rückkopplung

Wie Herr Knoll korrekt feststellt, ist die folgende Aussage irreführend:
Man sagt und liest allgemein: "Mit der Rückopplung wird der Kreis entdämpft und damit die Trennschärfe erhöht."
Anhand der von ihm geschilderten Beispiele ist experimentell leicht nachprüfbar, daß der Kreis selbst unverändert bleibt, sondern "nur" die Spannungen in der Schaltung sich ändern, wenn der Grad der Rückkopplung verändert wird.
Um die Wirkungsweise des rückgekoppelten Audions besser verstehen zu können, wird zunächst eine allgemeinere Form der Rückkopplung betrachtet, wie sie typisch für Regelkreise ist.
Zunächst muß der Begriff "Rückkopplung" präzisiert werden. Es gibt
- negative Rückkopplung = Gegenkopplung (i.a. bei Regelkreisen angewendet)
- positive Rückkopplung = Mitkopplung (z.B. beim Audion oder beim Oszillator angewendet)
Eine Blockstruktur, wie sie beispielsweise als Regelkreis vorkommt, zeigt das nächste Bild.

F(ω) ist die Eingangsgröße (Führungsgröße)
A(ω) ist die Ausgangsgröße
Z(ω) ist eine Störgröße (bei einer Regelung unerwünscht)
HR(ω) ist der "Regler" (Dieser muß so dimensioniert werden, daß die gesamte Schaltung vorgegebene Kriterien einhält.)
HS(ω) ist die "Stecke" (Das ist die vorgegene Schaltung, der mit Hilfe der Regelkreisstruktur ein bestimmtes Verhalten "verpaßt" werden soll.)
HG(ω) ist die "Rückführung" (in der Praxis oft ein Meßwandler, der die Ausgangsgröße in die gleiche Art [z.B. Spannung] wie die Eingangsgröße wandelt. Bei einem Operationsverstärker entspricht das der "äußeren Beschaltung".)
Σ ist eine "Summierstelle"
Wird die Rückführ-Schleife über "-" geschlossen, entsteht eine Gegenkopplung.
Wird die Rückführ-Schleife über "+" geschlossen, entsteht eine Mitkopplung.
Markiert sind die verschiedenen "Wege" der Signale.
- Vorwärts-Weg 1 (für die Eingangsgröße [Führungsgröße]): HV(ω)=HR(ω)HS(ω)
- Vorwärts-Weg 2 (für die Störung): HZ(ω)=1
- Schleifen-Weg = Kreisverstärkung: HO(ω)=HG(ω)HR(ω)HS(ω)
Für die Übertragungsfunktion GF(ω) bzw. GZ(ω) der obigen Regelkreisstruktur ergibt sich allgemein formuliert: Übertragungsfunktion = Vorwärts-Weg/(1± Schleifen-Weg) {"+" wenn "-" an der Summierstelle; "-" wenn "+" an der Summierstelle} :
GF(ω) = HV(ω)/(1±HO(ω))
GZ(ω) = HZ(ω)/(1±HO(ω))
Für den Spezialfall eines beschalteten Operationsverstärkers oder eines NF-Verstärkers mit Gegenkopplung, bei dem |HO(ω)| → "unendlich" geht, gilt damit:
GF(ω) = 1/HG(ω), Frequenzgang ist also nur noch von der äußeren Beschaltung abhängig.
GZ(ω) → 0 , also Störung (durch Nichtlinearitäten) verschwindet.
Nach dem Exkurs zu der Regelungstechnik nun zurück zu dem Problem mit dem Audion. Hier hat man i.a. eine positive Rückkopplung, also eine Mitkopplung. Wegen der Anschaulichkeit wurden folgende Vereinfachungen gemacht. Der Block H(ω) im Vorwärtsweg habe die Übertragungsfunktion eines Parallelschwingkreises, während der Rückführblock K frequenzunabhängig sein soll. Die gesamte Übertragungsfunktion des Audions wird mit G(ω) bezeichnet.

Für die Übertragungsfunktion H(ω) des Schwingkreises sei folgender Verlauf angenommen.
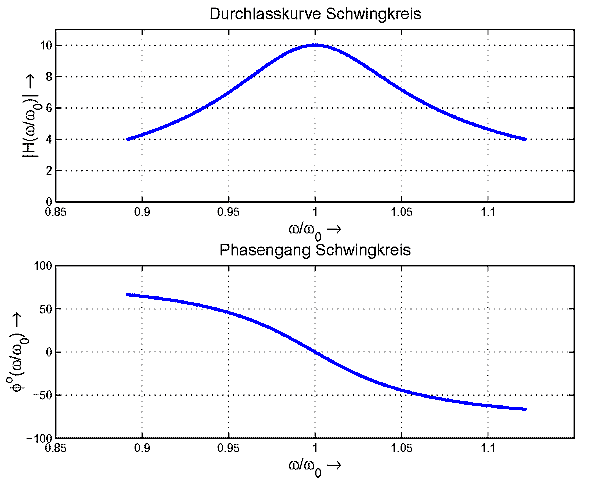
Die Schwingbedingung ist erreicht (das Audion "pfeift"), wenn die Kreisverstärkung H(ω)*K=1 wird. Da K frequenzunabhängig sein soll, wird die Schwingbedingung bei Vergrößerung des Wertes von K bei der Frequenz ω=ω0 erreicht (ω/ω0=1), wie aus der Resonanzkurve sofort erkennbar ist.
Eine Sinus-Schwingung der Frequenz ω0 erleidet beim Durchgang durch den Schwingkreis keine Phasendrehung, wie der Kurve des Phasengangs entnommen werden kann. Somit wird sie phasenrichtig an der Summierstelle addiert. Wenn nun die Kreisverstärkung bei der Frequenz ω0 genau gleich 1 ist (Grenzfall), wird keine Eingangsspannung mehr benötigt, um die Schwingung aufrecht zu erhalten.
Wie sieht das nun (bei gleichem Wert von K) bei Sinus-Schwingungen auf anderen Frequenzen aus, z.B. bei ω = 1,05ω0 ? (Das Audion soll (noch) nicht schwingen.)
Hier ist der Amplitudengang des Schwingkreises auf das ca. 0,7 fache des Maximalwertes abgefallen. Gleichzeitig hat die rückgeführte Spannung aber auch noch einen Phasenwinkel von ca. -450 Dadurch addieren sich die Spannungen nunmehr vektoriell, wodurch der Betrag der Summenspannung noch geringer wird.
Trägt man den Quotienten, also das Verhältnis, Ua(ω)/Ue(ω) = G(ω) auf, so ergibt sich damit der folgende Amplituden- und Phasengang für die mitgekoppelte Struktur G(ω) [der grün unterlegte Block], in Abhängigkeit von der Kreisverstärkung (hier K1 bezeichnet). 
Die stärkere Resonanzüberhöhung bei "angezogener" Rückkopplung entsteht durch die vektorielle Addition der einzelnen Frequenzkomponenten. Nur die Frequenzkomponente auf exakt der Resonanzfrequenz ω0 wird "phasenrein" addiert und liefert den größten Betrag, während alle sonstigen aufgrund der Dämpfung des Schwingkreises neben der Mittenfrequenz und wegen ihrer Phasendrehung nur geringere Beiträge liefern.
Man muß sich aber klar vor Augen halten, daß die Durchlaßkurven |G(ω)| aus einem Quotienten von Ausgangsspannung zu Eingangsspannung erhalten werden und nicht etwa durch eine physikalische Änderung des Schwingkreises H(ω). Dieser behält seine Eigenschaften bei - wird also tatsächlich nicht "entdämpft", unabhängig davon, wie groß die Mitkopplung K eingestellt wird.
Zum Schluß noch eine Anmerkung:
Wird das Vorzeichen von "+" nach "-" geändert, erhält man eine Gegenkopplung, wie ganz zu Anfang beschrieben. Es ist vielleicht von Interesse, daß ein Dreikreiser von 1938 eine Rückkoppelschaltung hat, die wahlweise als Mitkopplung oder als Gegenkopplung eingestellt werden kann. Letzteres natürlich für Ortsempfang.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Unterstuetzung von kompetenter Seite.

Hallo Leser im Forum.
Vor mehr als 5 Jahren habe ich diesen nicht ganz einfach zu verstehenden Beitrag mit diesen Worten eroeffnet:
Rein aus der Sicht des Technikers ein nicht ganz einfach zu beschreibendes Phänomen.
Die umfangreiche Literatur arbeitet da mit Formeln, Diagrammen und Kurven in grösserer Zahl
Dazu muss man sehen, das ist nicht die Materie mit der ich mein Brot verdient habe.
Audions waren vor meiner Zeit aktuell.
Nun ist mir jemand zu Hilfe gekommen, dem das Thema und seine physikalischen Hintergruende doch gelaeufiger sind als mir.
Ich mache kein Geheimniss daraus, dass ich sehr froh um diese spaete Bestaetingung meiner Vorstellungen und Gedanken. bin.
Danke! ist das Wenigste was ich noch beisteuern kann.
Das ist der Teamgeist der ersten Jahre im RMorg.
Hans M. Knoll
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Einfluss von Amplitudengang und Phasengang

Bei einem Schwingkreis sind die Form des Amplitudengangs und die Form des Phasengangs eindeutig miteinander verknüpft. Physikalisch lassen sich die Einflüsse der beiden auf die Übertragungsfuktion des Audions nicht auftrennen.
Diese Auftrennung geht jedoch in der Simulation, wo man keine Rücksicht auf physikalische Realisierbarkeit nehmen muß. [Das ist auch die Gefahr jeder Simulation, daß man aufpassen muß, um nicht an der physikalischen Realität vorbei zu simulieren!]
Für diese Simulationen wurden die Daten aus Post #2 verwendet. Das Blockschaltbild ist ebenfalls identisch.

Simulation 1: Amplitudengang wie der Schwingkreis, aber Phase identisch Null

Auch dieser (theoretische) Fall ergibt eine Resonanzüberhöhung bei ω0, die Abhängig vom Wert K1 der Kreisverstärkung ist. (Die Werte für K1 und die entsprechenden Farben sind identsich zu Post #2)
 Ein Vergleich mit dem Ergebnis mit dem realen Schwingkreis (Post #2) zeigt, daß die Resonanzüberhöhungen auf ω0, identische Werte erreichen, jedoch wegen der algebraischen statt der vektoriellen Addition in der Summierstelle die Resonanzkurven breiter werden.
Ein Vergleich mit dem Ergebnis mit dem realen Schwingkreis (Post #2) zeigt, daß die Resonanzüberhöhungen auf ω0, identische Werte erreichen, jedoch wegen der algebraischen statt der vektoriellen Addition in der Summierstelle die Resonanzkurven breiter werden.
Man sieht hier noch deutlicher als in Post #2, daß durch die "angezogene Rückkopplung" die Durchlaßkurve stets oberhalb der Durchlaßkurve ohne Rückkopplung liegt.
Das ist nochmals eine Bestätigung für den in Post #1 beschriebenen Effekt, daß eine "angezogene Rückkopplung" einen frequenzmäßig benachbarten Sender nicht schwächt!
Die "Weitab-Selektion" eines Audions sind also auch bei Rückkopplung nicht besser als es dem verwendeten Schwingkreis entspricht. Die oft vertretene Meinung, auf die Güte des verwendten Schwingkreises käme es bei einem Audion eigentlich gar nicht an, stimmt also nicht.
Simulation 2: Amplitudengang (Durchlaßkurve) rechteckförmig konstant, aber Phase wie der Schwingkreis

Bei der Summation sind jetzt alle Amplituden gleich, aber sie werden wegen der Phasendrehung vektoriell summiert.
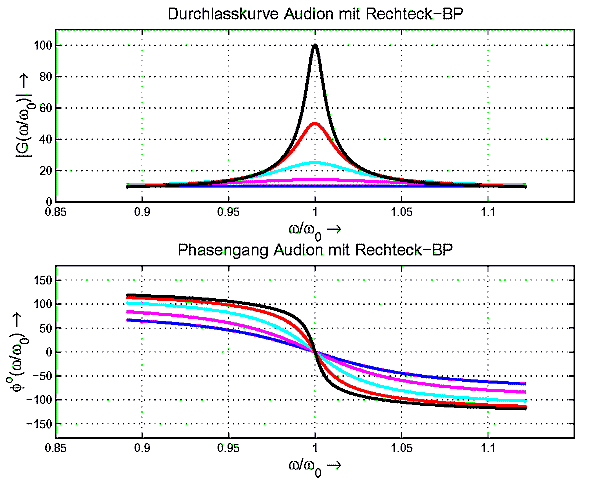
An diesen Kurven ist deutlich erkennbar, daß die Phase und damit die vektorielle Addition zu schmaleren Durchlaßkurven des Audions führt. Der Einfluß der Phase ist also größer als der der Amplitude des Schwingkreises!
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Schwingkreisgüte contra Rückkopplung

Theoretisch kann bei einem Audion ein Schwingkreis mit geringer Güte zum Einsatz kommen, da mit Hilfe der Rückkopplung das Audion so weit entdämpft werden kann, daß de facto eine Durchlaßkurve wie bei einem Schwingkreis mit sehr hoher Güte entsteht.
In der Praxis zeigt es sich aber, daß es vorteilhaft ist, die Güte des Schwingkreises möglichst hoch zu wählen.
Zum Nachweis der theoretischen Aussage werden berechnete Amplituden- und Phasenverläufe eines Schwingkreises und einer Audionschaltung mit einander verglichen.
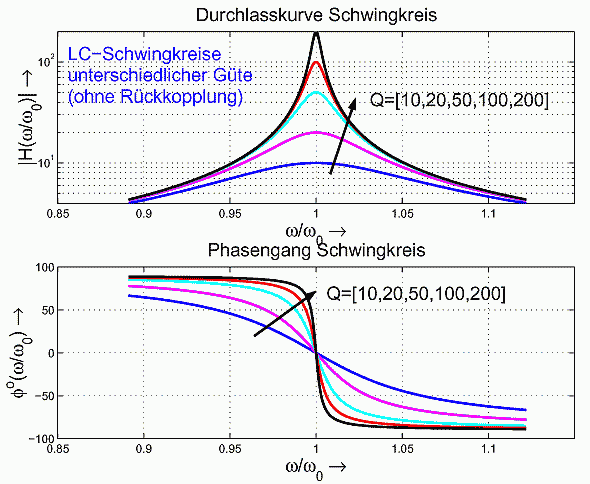
Die Güten der untersuchten Schwingkreise betragen Q = 10, 20, 50, 100, 200. Die Durchlaßkurven sind im logarithmischen Maßstab dargestellt, damit die Verläufe außerhalb der Resonanzfrequenz besser zu sehen sind.
Diese Kurven werden nun verglichen mit einer Mitkopplungs-Struktur (entsprechend zum rückgekoppelten Audion), wobei der verwendete Schwingkreis eine Güte Q=10 hat.

Die Rückkopplung (und damit die Kreisverstärkung K1) wird hierbei so gewählt, daß das Audion die gleichen Durchlaßkurven hat wie zuvor die Schwingkreise alleine. Und in der Tat, die beiden Kurvenscharen sind (bis auf Rundungsfehler bei der Berechnung) identisch.
Welche praktischen Überlegungen sprechen nun gegen die Verwendung eines Kreises geringer Güte beim Audion?
Geht man z.B. von einer Kreisgüte von Q=10 aus und soll durch die Mitkopplung die effektive Güte Qeff=100 erreicht werden, ist eine Kreisverstärkung K1=0,9 (90%) erforderlich. (Bei 100% Kreisverstärkung schwingt das Audion.) Ändert sich infolge von Spannungsschwankungen die Kreisverstärkung um z.B. +5% wird K1=0,95 und Qeff=200. Das ist eine Änderung von 100%.
Hat der Schwingkreis dagegen z.B. eine Güte von Q=50, ist nur eine Kreisverstärkung K1=0,5 notwendig, um auf Qeff=100 zu kommen. Ergibt sich nun eine Änderung der Kreisverstärkung um +5%, wird K1=0,55 und damit Qeff=50/0,45=111,1. Das ist eine Änderung von 11,1%.
Aus diesen Beispielen ist zu erkennen, daß die Empfindlichkeit eines Audions bezüglich Verstärkungsschwankungen (infolge von Spannungschwankungen, Temperaturschwankungen, Frequenzänderungen [Handempfindlichkeit] etc.) um so größer ist, je stärker die Rückkopplung "angezogen" werden muß, um auf eine gewünschte effektive Güte Qeff zu kommen. Audions mit Schwingkreisen geringer Güte lassen sich daher nur viel schwieriger bedienen.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Trennschärfe und Weitabselektion

Die Trennschärfe eines Empfängers, hier des Audions, wird wesentlich durch die Steigung der Durchlaßkurven des Schwingkreises außerhalb des Bereichs der Resonanzüberhöhung bestimmt. Da 1 Schwingkreis 2 Energiespeicher hat (L & C), kann die Steilheit der Durchlaßkurven asymptotisch, d.h. außerhalb des Bereiches mit der Resonanzüberhöhung, nur maximal ±20 dB/Dekade betragen. (+20dB/Dek. unterhalb von ω0 und -20dB/Dek. oberhalb)
Wie aus den Amplitudenkurven in Post #5 aufgrund der logarithmischen Darstellung erkennbar ist, trifft die obige Feststellung unabhängig von der Güte Q bzw. der (durch die Rükkopplung) eingestellten Kreisverstärkung K1 zu.
Das ist eine weitere Bestätigung für die im Post #1 festgestellte Unmöglichkeit, die Weitabselektion durch "Anziehen" der Rückkopplung zu verbessern.
Verwendet ein Empfänger 2 Schwingkreise (Zweikreiser) ist die asymptotische Steigung ±40dB/Dekade, und bei 3 Schwingkreisen (Dreikreiser) wird sie ±60dB/Dekade, usw. Man braucht also weitere Schwingkreise um die Weitabselektion zu verbessern.
Durch die Verwendung mehrerer Schwingkreise gibt es zusätzliche Freiheitsgrade, die es ermöglichen, die Form der Durchlaßkurve günstig (in Richtung rechteckförmig) zu beeinflussen. Da es in der Praxis unüberwindliche Schwierigkeiten bereitet, abstimmbare Filter mit vorgegebener Durchlaßkurve zu bauen, werden solche Filter auf einer festen Zwischenfrequenz realisiert, womit man dann beim Überlagerungsempfänger (Super) angekommen ist.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Rückgekoppelter Schwingkreis im Zeitbereich

Am Wochenende erreichte mich folgende Mail von einem Diplom-Physiker, der auch an der Radiotechnik Interesse hat. In der Anlage befand sich eine Berechnung des rückgekoppelten Schwingkreises mit Hilfe von Differentialgleichungen, also im Zeitbereich.
Sehr geehrter Herr Rudolph
Ich beziehe mich auf einige ihrer Beiträge auf der Website www radiomuseum.org vom März 2010 über die Frage, ob bei einem Rückkopplungsempfänger durch die Rückkopplung (Mitkopplung) die Trennschärfe und Weitabselektion gegenüber einem Einkreis-Geradeausempfänger erhöht werden können.
Herr Hans M. Knoll stellt Messungen vor, die den bekannten Ausspruch "Mit der Rückopplung wird der Kreis entdämpft und damit die Trennschärfe erhöht." in Zweifel ziehen. Sie bestätigen dies mit Hilfe der Theorie der Regeltechnik.
Neugierig geworden habe ich dies selbst nochmals aus einem anderen Blickwinkel, nämlich über die Differentialgleichungen des gedämpften rückgekoppelten bzw. nicht rückgekoppelten Schwingkreises, betrachtet und durchgerechnet. Die Schlußfolgerungen sind erfreulicherweise die selben.
Da diese Betrachtungen hoffentlich eine gute Ergänzung zum bisher zu diesem Thema von ihnen und von Herrn Knoll Gesagten sind, habe ich mich entschlossen meine Überlegungen als kurzen Artikel zusammenzuschreiben, den ich ihnen hiermit unterbreiten möchte. Sollten sie dies auch so sehen, so können sie diesen Artikel gerne auf www radiomuseum.org online stellen. Für etwaige Änderungen oder Anpassungen bin ich natürlich offen.
Mit freundlichen Grüßen
Jochen Bauer
Entdämpfung und Trennschärfe von Rückgekoppelten Schwingkreisen
Abstract
In der historischen Radiotechnik ist zu Rückkopplungsempfängern immer wieder der Ausspruch "Mit der Rückkopplung wird der Kreis entdämpft und damit die Trennschärfe erhöht“ zu hören und zu lesen. Die kritische Hinterfragung dieser Aussage ist auch Gegenstand eines Artikels auf der Website www radiomuseum.org . Darin wird diese Aussage sowohl experimentell, als auch mit Hilfe der Theorie der Regelungstechnik als irreführend bzw. falsch erkannt. Im vorliegenden Artikel soll dieser Sachverhalt nochmals aus einem anderen theoretischen Blickwinkel heraus mit Hilfe der Differentialgleichungen des gedämpften rückgekoppelten bzw. nicht rückgekoppelten Schwingkreises betrachtet werden.
Diese Analyse des rückgekoppelten Schwingkreises im Zeitbereich mit Hilfe von Differentialgleichungen (Multipage-PDF) ist eine interessante Bestätigung der von Hans Knoll und mir erfolgten Analyse im Frequenzbereich.
MfG DR
P.S. Wer sich für den Zusammenhang zwischen Differentialrgleichungen und komplexer Rechnung interessiert, kann das im Skript "Anwendungen der Laplace-Transformation" nachlesen.
Nachtrag 2
Der Zusammenhang zwischen der Betrachtung im Zeit- und Frequenzbereich wird auch am Beispiel des Teiler-Tastkopfes an elektronischen Meßgeräten ausführlich dargestellt. Dort ist das Skript zur Anwendung der Laplace-Transformation ebenfalls zu finden.
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.