Die Fourier-Analyse physikalisch

Auf die meisten Praktiker wirkt die Fourier-Analyse (und Synthese) wegen ihrer "Formel-Lastigkeit" eher abschreckend. In vielen Veröffentlichungen über dieses Thema findet man Beispiele für entsprechende Zerlegungen teils mit umfangreichen Formeln, teils auch mit einigen Graphiken. Auch eigentlich für Praktiker gedachte Veröffentlichungen, wie z.B. die Funktechnischen Arbeitsblätter machen da keine Ausnahme.

Man sieht hier jedoch das "Krümel-Formel-Gesetz", das viel Leute abschreckt:

"Je kleiner der Krümel, der berücksichtigt werden muß, umso größer ist die Formel, die zu seiner Beschreibung notwendig ist."

Im Unterschied dazu soll hier versucht werden, die physikalischen Aspekte der Fourier-Analyse zu zeigen. Wenn man diese verstanden hat, werden auch manche Formeln, ohne die es leider nicht ganz geht, dadurch verständlich.

Zu Beginn wird die Frage geklärt, was man in diesem Zusammenhang unter "Frequenz" versteht. Speziell hierzu findet man auch einen früheren Beitrag im RM.org.

Hier ist nun eine überarbeitete Fassung davon, bei der (noch) stärker  die physikalische Bedeutung der Fourier-Analyse herausgearbeitet ist.

---

Zunächst wird die "Resonanz" in der Akustik betrachtet.

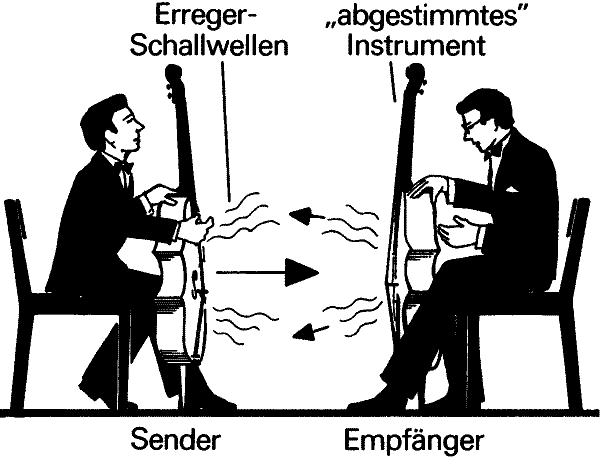
Man sieht hier ein "Sender"-Cello und ein auf das Sender-Cello abgestimmtes "Empfänger"-Cello. Macht man die im Empfänger-Cello angeregten Schwingungen der Saiten sichtbar, so hat man quasi eine Fourier-Analyse des Cello-Klanges.

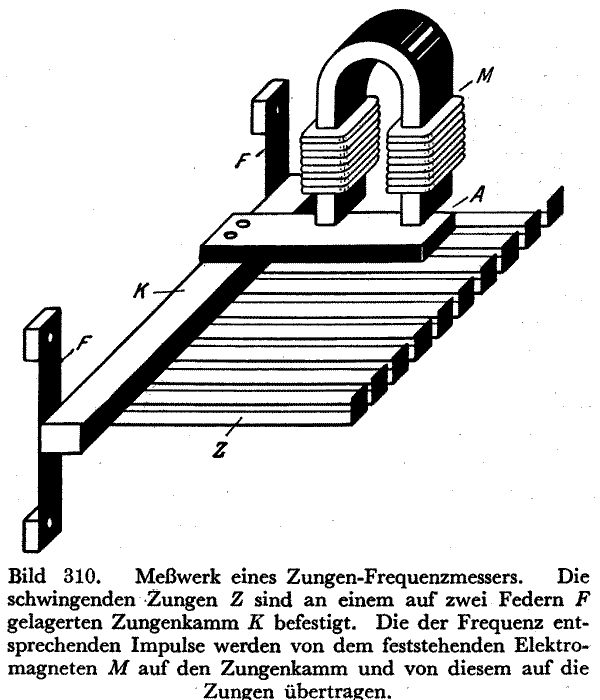
Ein Meßgerät, das diesen Effekt benutzt ist der Zungen-Frequenz-Messer.

Eine rein elektronische Lösung eines solchen Meßwerkes ist eine "Filterbank" aus parallel-geschalteten LC-Schwingkreisen.

Die (gemäß Fourier) frequenzmäßig zu analysierende Spannung s(t) wird (parallel) auf alle Filter dieser Filterbank gegeben. Die Resonanz-Frequenzen dieser Filter seien frequenzmäßig so gestaffelt, daß man da entlang eine Frequenzachse legen kann.

Die (sinusförmigen) Eigenschwingungen der jeweils erregten Filter werden in ihrer Amplitude und Phase bestimmt und ergeben so auf physikalische Weise die Fourier-Analyse der Spannung s(t).

Summiert man (z.B. mit Hilfe eines Summierverstärkers) die (Teil-) Schwingungen aller angeregten Filter, so erhält man ausgangsseitig die Synthese-Schwingung.

Während realisierbare Filter immer eine gewisse Bandbreite (und endliche Güte) haben, wird bei der Fourier-Analyse unterstellt, daß die Filter eine Bandbreite B = 0 haben (also infinitesimal schmal sein) sollen.

Die (theoretische) Voraussetzung B = 0 führt zu der Konsequenz, daß die Filter unendlich lange benötigen, bis sie eingeschwungen sind. Folglich müssen die Schwingungen, die diese (theoretischen) Filter überhaupt anregen können, ihrerseits auch unendlich lange andauern. Solche Schwingungsformen gibt es (idealisiert) tatsächlich. Es sind dies periodische Dauerschwingungen, wie der Sinus oder der Cosinus, die eben (theoretisch) unendlich lange andauern. 

Betrachtet man ein einzelnes Tiefpaßfilter, so erhält man gemäß dieser Überlegung eine Abschätzformel für die (minimal erforderliche) Einschwingzeit.

Wird auf den Eingang von einem Tiefpaß mit der Grenzfrequenz f_g eine Gleichspannung der Größe 1V angeschaltet (Sprungfunktion), so kann die Ausgangsspannung dieses Tiefpasses nicht schneller ansteigen, als es einer Sinus-Spannung der höchsten übertragenen Frequenz entspricht. Nimmt man das als Grenzwert, so ergibt sich t_{e min} = 1/(2f_g) .  Dies ist die in der Praxis benutzte Formel, wobei für f_g die 3dB Grenzfrequenz eingesetzt wird.

Unterstellt man eine Filterbank, deren Filter andere (als sinusförmige) Eigenschwingungen haben, z.B. rechteckförmige, so erhält man eine völlig andere Analyse, hier dann die "Walsh-Analyse".

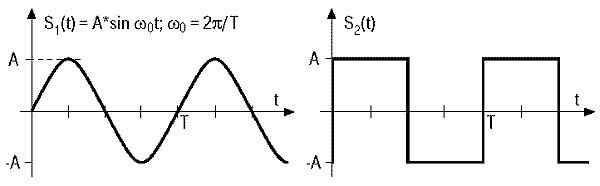
Aufgrund der heute so modernen "Digitalisierung" könnte man zur Auffassung gelangen, daß die Zerlegung einer Zeitfunktion in rechteckförmige Schwingungen mittel "Walsh-Analyse" viel wichtiger geworden sei als die konventionelle Fourier-Zerlegung in sinusförmige Schwingungen.

Aber mit Hilfe des Zusammenhangs zwischen Einschwingzeit und Bandbreite sieht mandaß zu einer unendlich scharfen Flanke eine unendlich hohe Grenzfrequenz gehört. Aber gerade im (Mobil-) Funkbereich  sind "Frequenzen" (Frequenzbänder) bekanntlich sehr sehr teuer. Man wird folglich nie "ideale" Sprünge realisieren können, sondern hat immer verrundete Flanken. Und damit sind wir wieder bei Fourier.

Die hier enthaltene Aussage "Δŧ·Δω = constant" ist das Zeit-Bandbreiten-Gesetz, ein Sonderfall der "Unschärfe-Relation".

Als Beispiel für eine (einseitige) Fourier-Analyse wird die Sägezahn-Schwingung betrachtet.

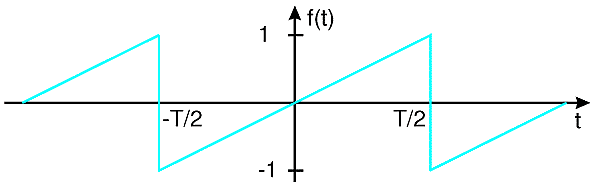
Diese technisch wichtige Zeitfunktion tritt z.B. als Ablenkspannung bei Oszilloskopen auf. Aber auch akustisch als Schwingungsform der Stimmbänder. Hier filtert dann der Nasen- und Rachenraum die Frequenzanteile aus, die zur Bildung der Vokale benötigt werden. Die Fourier-Analyse liefert die b-Koeffizienten (Amplituden) für die darin enthalteten Sinus-Schwingungen. (Negative Koeffizienten bedeuten gegenphasige Schwingungen.)

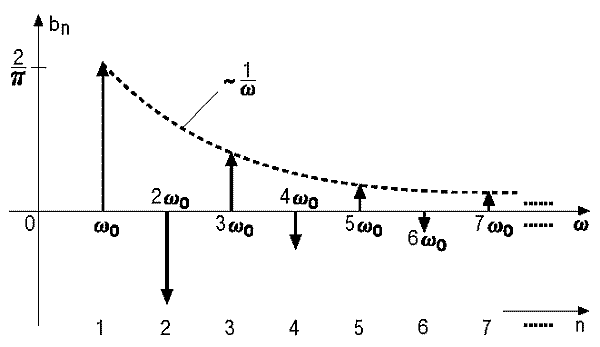
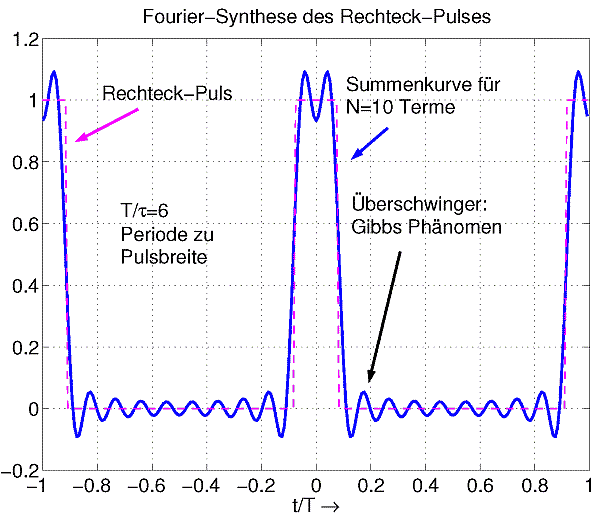
Die aus diesen Sinusschwingungen synthetisierte Sägezahn-Schwingung des nächsten Bildes zeigt, daß die Fourier-Analyse an Sprungstellen gewisse Ungenauigkeiten aufweist, die in den Synthese-Kurven mit "Gibbs'schem Phänomen" bezeichnet werden.

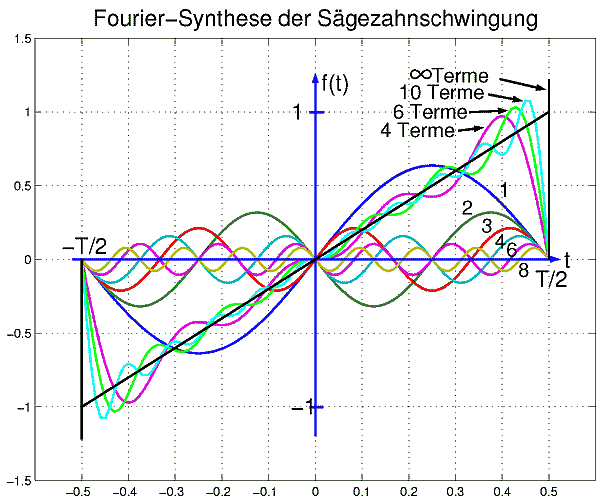
Auch bei Berücksichtigung von unendlich vielen Sinus-Schwingungen aus der Zerlegung verschwindet der Überschwinger (theoretisch) nicht.

Harmonische Schwingungen, wie Sinus oder Cosinus, können geometrisch als Projektionen einer sich drehenden Scheibe (mit einer Markierung) auf eine Achse interpretiert werden.

Hier hat man einen "Zeiger" (auf der Scheibe)  der Länge a₁. Die Scheibe läuft (gleichmäßig) mit der Winkel-Geschwindigkeit ω₀ in mathematisch positiver Richtung (gegen den Uhrzeiger) um. Die auf die senkrechte Achse projizierte Spitze des Zeigers beschreibt dann eine Cosinus-Kurve, wie sie rechts über der Zeit-Achse (bzw. alternativ: Achse des Winkels φ₁) aufgetragen ist.

Statt der Projektion auf einen Zeiger der Länge a₁ kann man sich auch eine "Scheren"-Mechanik aus zwei gegenläufigen Zeigern halber Länge a₁/2 vorstellen.

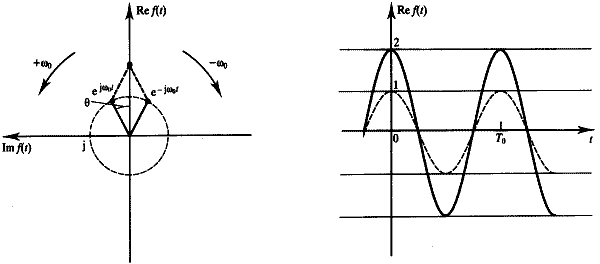
Damit die "Schere" immer auf der senkrechten Achse (R_e f(t)) bleigt, müssen die beiden Ziger mit der Winkel-Geschwindigkeit +ω₀ und -ω₀ umlaufen. (mathematisch positiv bzw. negativ) Auf diese Weise wird eine "negative Frequenz" definiert und entsprechend auf einer Frequenz-Achse aufgetragen. Der Vorteil dieser Darstellung besteht darin, daß Symmetrien im Spektrum deutlicher zu sehen sind. Aber auch bei der Beschreibung von Spektren modulierter Signale ergeben sich Vorteile, weil es dadurch übersichtlicher wird.

Als Beispiel für diese zweiseitige Fourier-Analyse wird der Rechteck-Puls-Zug betrachtet.

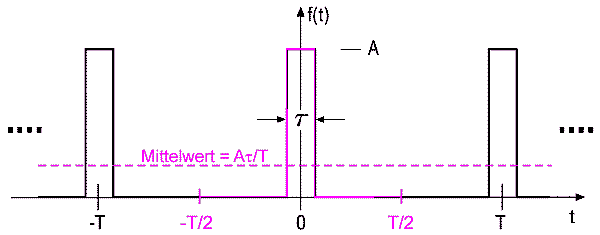
Dies ist der Proto-Typ z.B. für Digital-Signale. Aber auch Pulsfomen mit verrundeten Flanken können näherungsweise durch (flächengleiche) Rechteck-Impulse dargestellt werden. Folglich werden sich in solchen Fällen die Spektren dann auch nicht allzu wesentlich unterscheiden.

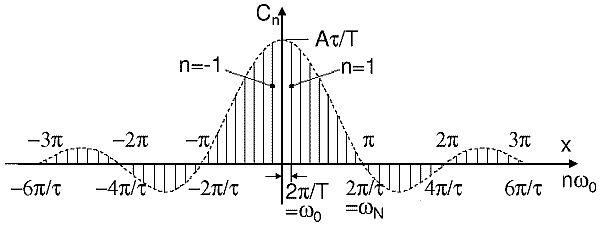
Hier sind die C_n Koeffizienten ( entsprechend der Zeiger halber Länge) aufgetragen. Man erkennt eine gerade Symmetrie (Spiegel-Symmetrie). Diese Symmetrien vereinfachen immer die Berechnung.

In der Synthese-Kurve treten wieder die Überschwinger als Gibbs'sches Phänomen hervor.

Wie  aus der Darstellung des Spektrum zu sehen ist, läßt sich dieses ganz einfach konstruieren, wenn man die Form der Hüllkurve (in diesem Beispiel in sin(x)/x ) kennt. Man braucht dann nur noch Linien im (gegenseitigen) Abstand ω₀ = 2π/T bis zur Hüllkurve zu zeichnen und hat das gesuchte Ergebnis.

Die Form der Hüllkurve im Spektrum hängt von der Form des Einzel-Impulses ab. Werden nur Einzel-Impulse betrachtet, oder allgemeiner endlich andauernde Zeitsignale, so kommt man zur Fourier-Transformation.

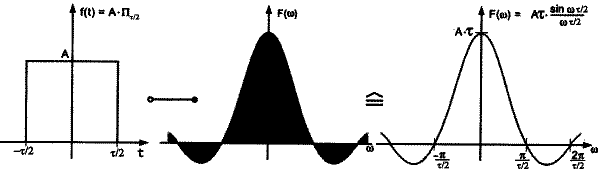
Aufgrund des Zeit-Bandbreiten-Gesetzes liegen in einem sochen Fall die Linien im Spektrum dann so dicht neben einander, daß eigentlich die gesamte Fläche unter der Kurve schwarz auszufüllen wäre. Man beschränkt sich deshalb auf die Darstellung der Hüllkurve (die man ja sowieso nur wollte).

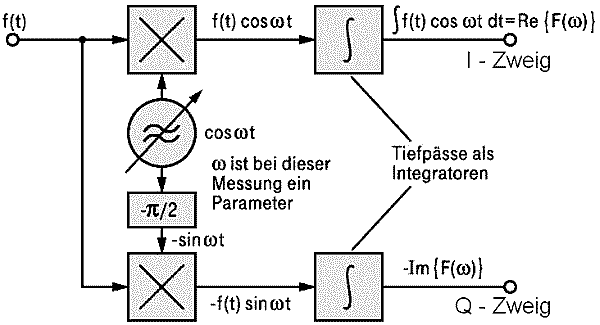
Die Formel, die der Fourier-Transformation zugrunde liegt, ist eine Verallgemeinerung der zweiseitigen Fourier-Analyse. Diese Formel läßt sich dann in ein Blockschaltbild übersetzen und liefert damit das Prinzip-Schaltbild eines Spektrum-Analysators.

In der Anlage ist eine ausführlichere Beschreibung der hier vorgestellten Zusammenhänge zu finden.

Fourier-Analyse physikalisch (pdf 1,8MB)

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.