freed-eise: Hazeltine-Winkel; magic angle

Der Hazeltine-Winkel.

Die Hazeltinesche Neutralisation behebt das Problem der kapazitiven Verkopplung zwischen Gitter- und Kathodenkreis, verursacht durch die Gitter-Anodenkapazität bei Trioden. Es verbleibt aber die induktive Kopplung, die vor allem bei höheren Kreisgüten und höherer Stufenverstärkungauch zu Unstabilität / Schwingneigung führen kann.

Hazeltine postuliert in seiner Patentschrift eine parallele Schrägstellung der Spulen um 54.7° mit einer Formel, die nicht weiter begründet wird.
Die von Hazeltine vorgegebenen Werte wurden seinerzeit von Hazeltines Lizenznehmern fast durchwegs befolgt. Früheste Modelle wie Freed-Eisemann NR-5 und NR-6 zeigen den typischen Aufbau, wie er jahrelang angewandt wurde bei nicht abgeschirmten Spulen (bei abgeschirmten Spulen besteht keine induktive Kopplung).
Fußpunktabstand = 6“
SpulenØ = 3“
Länge der äußeren Wicklung = ca. 2“
Schrägstellung = 54,7°
In der FG 209 wurde versucht, die klassische Grösse 54,7° nachzuvollziehen.
Überraschenderweise ergab sich mit 48°eine erhebliche Abweichung!
Dies veranlasste uns, ebenfalls Versuche anzustellen.

Achim Korn erklärte sich bereit einen Versuchsaufbau zu schaffen und Messungen durchzuführen.
Ausgehend von den Originalgrößen:
Spulendurchmesser 3";
66 Windungen 0.5 mm gleichmässig auf 48 mm verteilt (durch mitgeführte Nylonschnur), Induktivität 290 µH;
Fußpunktabstand zwischen den Spulen original 6", wurde variiert zu 5", 6", 7", 8";
Nur die Kreisspulen wurden nachgebildet. Die Ankoppelspulen wurden weggelassen, denn bei der sehr festen Kopplung zwischen den übereinander liegenden Wicklungen kann deren Feldausbildung praktisch als identisch angenommen werden.

Die Sekundärspule wurde mit einem Drehkondensator abgestimmt.
Die Messungen erfolgten bei drei Frequenzen:  500 kHz, 750 kHz, 1000 kHz.

Bei drei Spulen im Schwingzustand ist der Fall unübersichtlich: was koppelt wohin? Die Messung zwischen zwei Spulen ist eindeutiger.

Die primäre Spule (normalerweise anodenseitig) wurde aus einem Messgenerator gespeist. An der sekundären Spule (normalerweise gitterseitig) auf Resonanz abgestimmt, wurde die HF-Spannung oszillografisch gemessen.

Bei 500 kHz ergaben sich für die Abstände 5 / 6 / 7 / 8 " folgende optimalen Winkel: 55,0 / 54,0 / 52,5 / 51,5°
bei 750 kHz waren es 52,5 / 50,5 / 48,5 / 47,0°
und bei 1000 kHz : 49,5 / 46,0 / 42,5 / 39,5°

Nur bei 500 kHz und 6" Abstand zeigt sich einigermaßen Übereinstimmung mit den 54,7°.
Das lässt den Schluss zu, dass die in FG 209 berichteten Messungen auf nicht modellgerechten (maßstäblichen) Werten beruhen.
Vermutlich wurde bei höherer Frequenz als 500 kHz gemessen.

Herr Alfred Stoll, GFGF, der in FG 188 das Thema behandelte, unternahm die theoretische Berechnung über die Gegeninduktivität nach einem Buch von Grover. Dort wird ausdrücklich darauf hingewiesen, dass die Rechnungen nur bei sehr niedrigen Frequenzen gültig sind. Korrekturen für höhere Frequenzen werden nur für Induktivitätsberechnungen (Selbstinduktion) angeboten.
Aber die Ergebnisse liegen schon nahe am Originalwert bei 500 kHz:
Bei 5 / 6 / 7 / 8" sind es 56,6 / 56,1 / 55,7 / 55,5°. Die Frequenz scheint dabei schon Einfluss zu zeigen.
Winkel berechnet 56,1°
Winkel gemessen 54,0°
Winkel angewandt 54,7°

Fazit: maßstäbliche Modellversuche haben ihre Tücken!

Mein Dank gilt den Herren Alfred Stoll und Achim Korn.
Konrad Birkner

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Sucht man nach Magic Angle findet man u.a. in Wikipedia die folgende Definition:

θ_m = arccos(1/√3 ) = arctan √2 ≈ 54.7356°

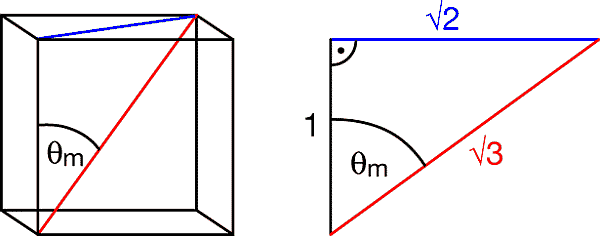
Könnte das die Begründung für die Wahl des Winkels von ca. 55⁰ durch Hazeltine sein?

Interessant ist, daß dieser Winkel auch sonst noch in der Physik im Zusammenhang mit der Magneto- Resonanz vor kommt.

Hat dieser "Magische Winkel" universellere Bedeutung? Wenn ja, warum?

Bei "Wigge, H.: Rundfunktechnisches Handbuch, 2. Teil, Krayn, 1927" wird der entsprechende Winkel gemäß der nachfolgenden Skizze eingestellt, wobei sich ca. 60⁰ ergeben.

Ein Dreikreiser sieht damit konstruktiv so aus:

Wie zu erkennen ist, gibt es hier eine relativ einfache Vorschrift zur Montage:

• Die Oberkante der vorherigen Spule fluchtet mit der Unterkante der nachfolgenden Spule.

Das ist eine Vorschrift, die auch der (ungelernte) Bastler bzw. der Monteur am Fließband relativ einfach einhalten kann. Fernerhin ist durch optische Inspektion eine einfache Kontrolle möglich.

Nach der Theorie ist offensichtlich so keine exakte Entkopplung möglich. Gut, aber die Theorie erfaßt auch nicht die kapazitiven Verkopplungen z.B. durch die Leitungsführung. Und die Kapazitäten der (damals noch handgefertigten) Röhren können ebenfalls nicht mathematisch in einem entsprechenden Modell berücksichtigt werden.

Der "magische Winkel" kann hier also nur als Richtwert dienen. Die eigentliche Entkopplung der gesamten Schaltung (damit keine Rückkopplung auftritt und sie schwingt) geschieht durch Neutralisation. Es ist das Verdienst von Hazeltine, eine entsprechende Brückenschaltung angegeben zu haben, die mit Hilfe von "Neutrodons" (die beiden "Röhrchen" auf dem Panel vor den Spulen) abgegelichen wird.

Da aufgrund des wenigstens ungefähr stimmenden "magischen Winkels" die Verkopplung gering ist, läßt sich die Neutralisation entsprechend einfach einstellen.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Zur Ergänzung zitiere ich aus meiner Korrespondenz mit Herrn Alfred Stoll:

Zitat___
1) U.S.Patent Nr. 1,577,421, erteilt 3/16/1926, eingereicht 4/7/1924, Patentinhaber Louis Hazeltine:
"Means for eliminating magnetic coupling between coils.

2) Frederick W.Grover: Inductance calculations, working formulas and tables, D.van Nostrand Co., New York, 1946, 286 Seiten.
Im Kapitel 21 "Circuit elements of larger cross sections with parallel axes" wird gezeigt, dass Kopplung null von den Windungszahlen und allen Abmessungen in recht komplizierter Weise abhängt.

___Zitat Ende

In der Anlage Auszüge aus dem Buch von Grover, die Herr Stoll freundlicherweise kopierte.Er führte auch die Berechnungen durch nach den Formeln (184) und (187) unter Verwendung der Originalabmessungen (s.o.) und für die Abstände 5" / 6" / 7" / und 8", wobei beide Formeln übereinstimmend (!) folgende Winkel ergaben: 56,6° / 56,1° / 55.7° und 55,5°.

Hier sind die relevanten Seiten aus Grover zu finden

 

Dank an Achim Korn für den Versuchsaufbau und die Durchführung der Messungen (siehe Anlagen).

Anlagen:

• Messaufbau (227 KB)
• Messergebnisse (3 KB)

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Beispiel im Stromberg Carlson 1A

Die interessanten Ausführungen haben mich motiviert, bei meinem Stromberg Carlson 1A  die Stellung der Spulen zu messen. Stromberg Carlson ist einer meiner Favoriten was Präzision in der mechanischen Verarbeitung betrifft. Stromberg Carlson ist auch Patentnehmer von Hazeltine. Der gemessene Winkel bei allen 3 Spulen ergibt einen Mittelwert von 55° was sehr genau dem Wert der Patentschrift (54.7°) entspricht.

Um keine Probleme bei der Montage zu haben, wurde eine diagonale Befestigungs- Verschraubung gewählt. Siehe Foto. Ein guter Weg wie Präzision und Serienfertigung vereinbart werden kann.

Gruß Wolfram Zylka

 

Anlagen:

• Spulen Winkel 2 (58 KB)

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Hazeltine hat in seiner Patentschrift 1,577,421 vom 16. März 1926 eine Begründung für den von ihm gefundenen "Magischen Winkel" von ca. 55⁰ angegeben, die genau der geometrischen Konstruktion der Diagonale in einem Würfel entspricht, s. Post #2.

Im Anhang ist ein Auszug aus der Patenschrift von Hazeltine zu finden, der die Begründung für seine Erfindung wiedergibt. (OCR, auf Englisch)

Hazeltine wählt zur Herleitung eine Idealisierung, die auf einen einfachen Zusammenhang führt. (Es kommen also nicht die Grooverschen Formeln zum Tragen.)

Als Ergebnis folgt für den Winkel, bei dem die Kopplung theoretisch verschwindet, der Wert 54,7⁰.

In der Figur 2a zeigt er, wie die Spulen vorteilhaft auf ihren jeweilgen Drehkos zu montieren sind, damit die Spulen unter dem richtigen Winkel zu einander stehen.

Man beachte die beiden Neutralisierungs-Kondensatoren C_n. Hiermit werden die kapazitven Verkopplungen der Schaltung (in einer Brückenschaltung) "neutralisiert". Hazeltine betont, daß die Neutralisation nicht zur Kompensation der magnetischen Verkopplung "mißbraucht" werden darf, weil sonst keine Frequenzunabhängigkeit  erreichbar ist.

Zur Verdeutlichung des Winkels der Spulen ist dieser in Fig. 2b gezeichnet.

Hazeltine betont, daß diese Konstruktion auch für mehr als 3 Spulen funktioniert.

Ein Detail von Drehkondensator und Spule zeigt die nächste Figur.

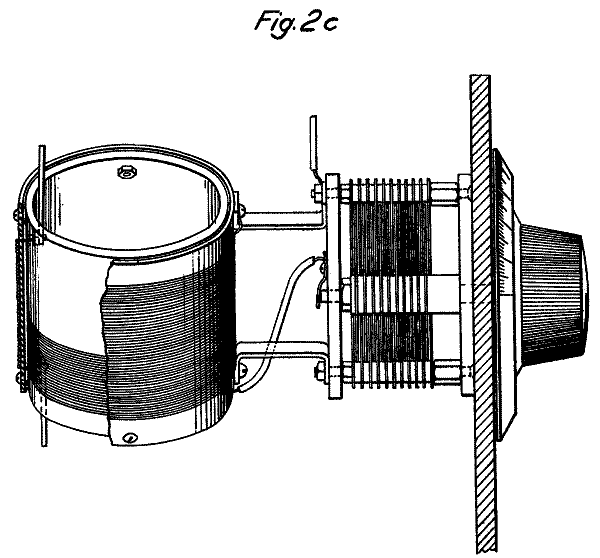
In der Schaltung ist erkennbar, daß die Sulen T2 und T3 tatsächlich Hochfrequenz-Transformatoren sind. (Ist auch schon in Fig. 2a erkennbar.)

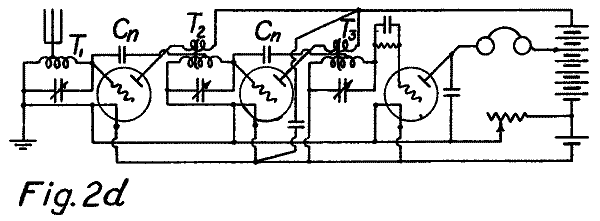
Aufgrund des kleinen Innenwiderstandes der (damals benutzten) Trioden hat die Primärwicklung dieser Transformatoren jeweils wenige Windungen (ist aperiodisch) während die Sekundärwicklung zusammen mit dem jeweilgen Drehko den Schwingkreis bildet und viele Windungen aufweist. Auf die magnetische Verkopplung hat also die Sekundärwicklung den entscheidenden Einfluß.

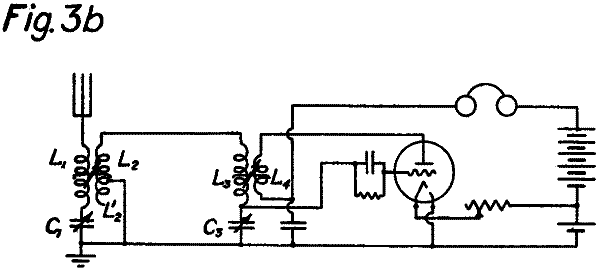
Das Prinzip der unter dem Winkel von ca. 55⁰ entkoppelten Spulen kann auch für Empfänger mit Rückkopplung vorteilhaft verwendet werden. Fig. 3a zeigt einen Aufbau und Fig. 3b die zugehörige Schaltung.

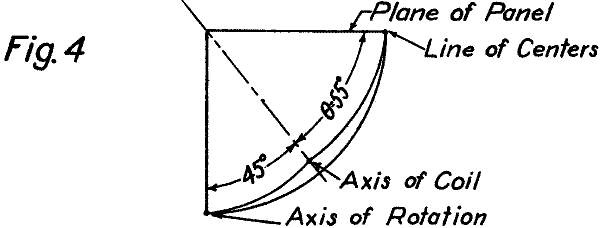
In der abschließenden Figur 4, die man sich 3-dimensional (wie den Würfel aus Post#2) vorstellen muß,  wird der "Magische Winkel" von 55⁰ hervorgehoben.

 

Weitere Details können der Beschreibung von Hazeltine (pdf, 185kB)  entnommen werden. Dort ist auch der Link zum Download der Patentschrift angegeben.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Der "Magic Angle" arccos(1/sqrt(3))=54.735...° ist tatsächlich ein universeller Winkel, der bei vielen Phänomenen auftritt, die mit der Wechselwirkung von magnetischen Dipolen zu tun haben. Das dahinter stehende Prinzip ist aber recht einfach:

Wir gehen von zwei kurzen Spulen aus, deren Achsen parallel zueinander sind.

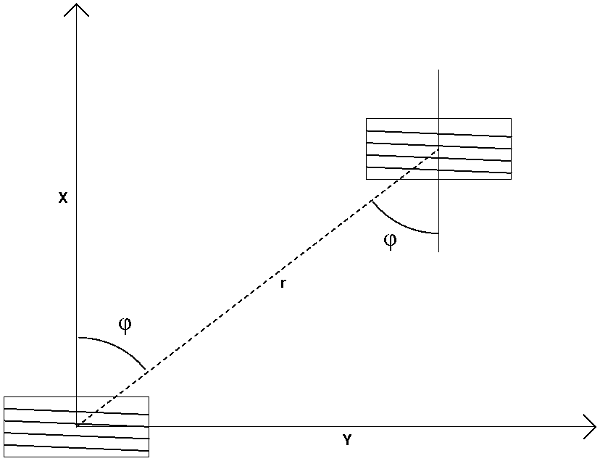
Die erste Spule kann bequemerweise in den Ursprung des Koordinatensystems mit der Spulenachse entlang einer der Koordinatenachsen gelegt werden. Die zweite Spule befindet sich an einem anderen Punkt in der Ebene, die die beiden Spulen enthält.

Die Frage ist nun: An welchen Stellen in der Ebene kann die zweite Spule liegen, damit die magnetische Kopplung zwischen beiden Spulen verschwindet? Immer unter der Voraussetzung, dass die beiden Spulenachsen parallel zueinander sind.

Für Spulen mit verschwindend geringer Ausdehnung (genau genommen im mathematischen
Grenzübergang für Spulenausdehnung -> 0) kann diese Frage sehr einfach und vor allem exakt, d.h. ohne eine Näherung, beantwortet werden: Die magnetische Kopplung verschwindet an allen Stellen, an denen der Winkel zwischen der Verbindungslinie der beiden Spulen und den Spulenachsen eben dieser "Magic Angle" ist (siehe Zeichnung), unabhängig vom Abstand r der beiden Spulen.

Die Herleitung dieses Magic Angle ist mit Hilfe des exakten Ausdrucks für das B-Feld des magnetischen Dipols im Raum sehr leicht zu machen und für den interessierten Leser diesem Post als PDF Dokument angehängt.

Dieses Magic Angle Prinzip ist exakt gültig, wenn die Spulen eine verschwindend geringe Ausdehnung haben und die Magnetfelder statisch sind. Näherungsweise gilt es auch noch für hinreichend niedrige Frequenzen und wenn der Abstand der Spulen hinreichend groß zu deren Ausdehnung ist. Wie manches mal in der Physik zeigt sich auch hier, dass eine Näherung noch für Anordnungen (Abstand/Ausdehnung) "halbwegs brauchbar" ist, bei denen man es gar nicht mehr erwarten würde. Eine Bemerkung dazu findet sich auch in der im Post #5 referenzierten Patentschrift von Hazeltine:

"[...] applies strictly only when the coils are far apart relative to their dimensions, yet it has been found by experiment that coils whose axial length is two-thirds their diameter may be brought almost into contact without changing the value of the angle for zero coupling by more than a very few degrees"

Zur genaueren Berechnung des Magic Angle bei großen Spulen und geringem Abstand muss auf
weitere Näherungsverfahren zurückgegriffen werden. Üblicherweise bedient man sich hier der
Multipolentwicklung für Magnetfelder und erhält damit Korrekturterme zum Magic Angle, die in der Regel von der Spulengeometrie und vom Spulenabstand abhängig sind.

 

Anlagen:

• Herleitung Magic Angle (29 KB)

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.